The Planck distribution
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
246-247
2025-11-19
42
The Planck distribution
The German physicist Max Planck studied black-body radiation from the viewpoint of thermodynamics. In 1900 he found that he could account for the experimental observations by proposing that the energy of each electromagnetic oscillator is limited to discrete values and cannot be varied arbitrarily. This proposal is quite contrary to the viewpoint of classical physics (on which the equipartition principle used by Rayleigh is based), in which all possible energies are allowed. The limitation of energies to discrete values is called the quantization of energy. In particular, Planck found that he could account for the observed distribution of energy if he supposed that the permitted energies of an electromagnetic oscillator of frequency ν are integer multiples of hν:
E=nhν n=0, 1, 2, ...
where h is a fundamental constant now known as Planck’s constant. On the basis of this assumption, Planck was able to derive the Planck distribution:
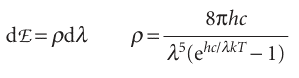
(For references to the derivation of this expression, see Further reading.) This expression fits the experimental curve very well at all wavelengths (Fig. 8.7), and the value of h, which is an undetermined parameter in the theory, may be obtained by varying its value until a best fit is obtained. The currently accepted value for h is 6.626 × 10−34 J s.
The Planck distribution resembles the Rayleigh–Jeans law (eqn 8.3) apart from the all-important exponential factor in the denominator. For short wavelengths, hc/λkT >> 1 and ehc/λkT →∞faster than λ5→0; therefore ρ →0 as λ→0 or ν→∞. Hence, the energy density approaches zero at high frequencies, in agreement with observation. For long wavelengths, hc/λkT << 1, and the denominator in the Planck distribution can be replaced by
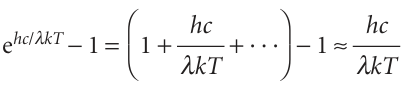
When this approximation is substituted into eqn 8.5, we find that the Planck distribution reduces to the Rayleigh–Jeans law. It is quite easy to see why Planck’s approach was successful while Rayleigh’s was not. The thermal motion of the atoms in the walls of the black body excites the oscillators of the electromagnetic field. According to classical mechanics, all the oscillators of the f ield share equally in the energy supplied by the walls, so even the highest frequencies are excited. The excitation of very high frequency oscillators results in the ultraviolet catastrophe. According to Planck’s hypothesis, however, oscillators are excited only if they can acquire an energy of at least hν. This energy is too large for the walls to supply in the case of the very high frequency oscillators, so the latter remain unexcited. The effect of quantization is to reduce the contribution from the high frequency oscillators, for they cannot be significantly excited with the energy available.
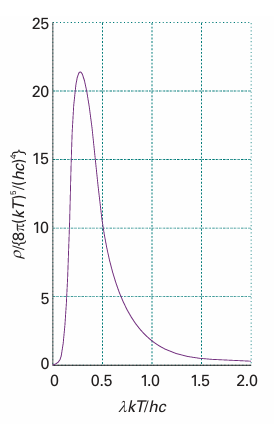
Fig. 8.7 The Planck distribution (eqn 8.5) accounts very well for the experimentally determined distribution of black-body radiation. Planck’s quantization hypothesis essentially quenches the contributions of high frequency, short wavelength oscillators. The distribution coincides with the Rayleigh–Jeans distribution at long wavelengths.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
