Black-body radiation
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص244-246
2025-11-19
33
Black-body radiation
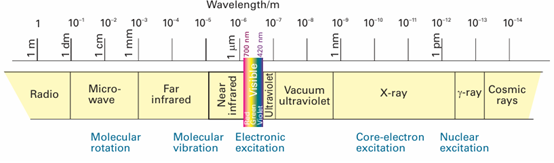
A hot object emits electromagnetic radiation. At high temperatures, an appreciable proportion of the radiation is in the visible region of the spectrum, and a higher
proportion of short-wavelength blue light is generated as the temperature is raised. This behaviour is seen when a heated iron bar glowing red hot becomes white hot when heated further. The dependence is illustrated in Fig. 8.3, which shows how the energy output varies with wavelength at several temperatures. The curves are those of an ideal emitter called a black body, which is an object capable of emitting and absorbing all frequencies of radiation uniformly. A good approximation to a black body is a pinhole in an empty container maintained at a constant temperature, because any radiation leaking out of the hole has been absorbed and re-emitted inside so many times that it has come to thermal equilibrium with the walls (Fig. 8.4). The explanation of black-body radiation was a major challenge for nineteenth century scientists, and in due course it was found to be beyond the capabilities of classical physics. The physicist Lord Rayleigh studied it theoretically from a classical viewpoint, and thought of the electromagnetic field as a collection of oscillators of all possible frequencies. He regarded the presence of radiation of frequency ν (and therefore of wavelength λ = c/ν) as signifying that the electromagnetic oscillator of that frequency had been excited (Fig. 8.5). Rayleigh used the equipartition principle (Section 2.2) to calculate the average energy of each oscillator as kT. Then, with minor help from James Jeans, he arrived at the Rayleigh–Jeans law (see Further reading for its justification):
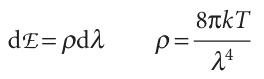
where ρ (rho), the density of states, is the proportionality constant between dλ and the energy density, dE, in the range of wavelengths between λ and λ + dλ, k is Boltzmann’s constant (k = 1.381 × 10−23 J K−1). The units of ρ are typically joules per metre4 (J m−4), to give an energy density dE in joules per cubic metre (J m−3) when multiplied by a wavelength range dλ in metres. A high density of states at the wave length λ simply means that there is a lot of energy associated with wavelengths lying between λ and λ +dλ. The total energy density (in joules per cubic metre) in a region is obtained by integrating eqn 8.3 over all wavelengths between zero and infinity, and the total energy (in joules) within the region is obtained by multiplying that total energy density by the volume of the region.
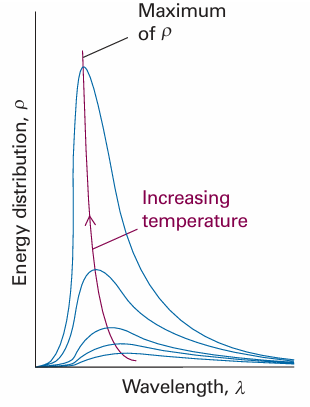
Fig. 8.3 The energy distribution in a black body cavity at several temperatures. Note how the energy density increases in the region of shorter wavelengths as the temperature is raised, and how the peak shifts to shorter wavelengths. The total energy density (the area under the curve) increases as the temperature is increased (as T4).
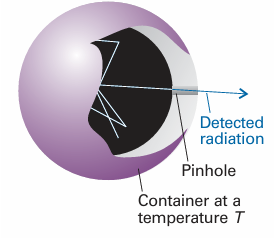
Fig. 8.4 An experimental representation of a black-body is a pinhole in an otherwise closed container. The radiation is reflected many times within the container and comes to thermal equilibrium with the walls at a temperature T. Radiation leaking out through the pinhole is characteristic of the radiation within the container.
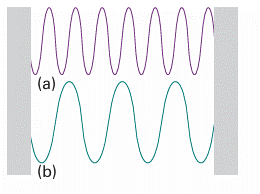
Fig. 8.5 The electromagnetic vacuum can be regarded as able to support oscillations of the electromagnetic field. When a high frequency, short wavelength oscillator (a) is excited, that frequency of radiation is present. The presence of low frequency, long wavelength radiation (b) signifies that an oscillator of the corresponding frequency has been excited.
Unfortunately (for Rayleigh, Jeans, and classical physics), although the Rayleigh Jeans law is quite successful at long wavelengths (low frequencies), it fails badly at short wavelengths (high frequencies). Thus, as λ decreases, ρ increases without going through a maximum (Fig. 8.6). The equation therefore predicts that oscillators of very short wavelength (corresponding to ultraviolet radiation, X-rays, and even γ-rays) are strongly excited even at room temperature. This absurd result, which implies that a large amount of energy is radiated in the high-frequency region of the electromagnetic spectrum, is called the ultraviolet catastrophe. According to classical physics, even cool objects should radiate in the visible and ultraviolet regions, so objects should glow in the dark; there should in fact be no darkness.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
