Gaussian Integral
المؤلف:
Guitton, E.
المصدر:
"Démonstration de la formule." Nouv. Ann. Math. 65
الجزء والصفحة:
...
28-4-2019
3568
Gaussian Integral
The Gaussian integral, also called the probability integral and closely related to the erf function, is the integral of the one-dimensional Gaussian function over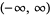 
. It can be computed using the trick of combining two one-dimensional Gaussians
Here, use has been made of the fact that the variable in the integral is a dummy variable that is integrates out in the end and hence can be renamed from 
to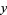 
. Switching to polar coordinates then gives
There also exists a simple proof of this identity that does not require transformation to polar coordinates (Nicholas and Yates 1950).
The integral from 0 to a finite upper limit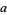 
can be given by the continued fraction
where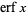 
is erf (the error function), as first stated by Laplace, proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).
The general class of integrals of the form
 |
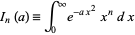(9)
|
can be solved analytically by setting
Then
For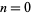 
, this is just the usual Gaussian integral, so
 |
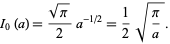(15)
|
For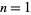 
, the integrand is integrable by quadrature,
![I_1(a)=a^(-1)int_0^inftye^(-y^2)ydy=a^(-1)[-1/2e^(-y^2)]_0^infty=1/2a^(-1).](http://mathworld.wolfram.com/images/equations/GaussianIntegral/NumberedEquation3.gif) |
(16)
|
To compute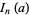 
for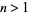 
, use the identity
For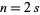 
even,
so
where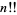 
is a double factorial. If 
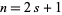is odd, then
so
 |
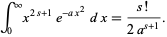(33)
|
The solution is therefore
![int_0^inftye^(-ax^2)x^ndx=<span style=]() {((n-1)!!)/(2^(n/2+1)a^(n/2))sqrt(pi/a) for n even; ([1/2(n-1)]!)/(2a^((n+1)/2)) for n odd. " src="http://mathworld.wolfram.com/images/equations/GaussianIntegral/NumberedEquation5.gif" style="height:98px; width:286px" /> |
(34)
|
The first few values are therefore
A related, often useful integral is
 |
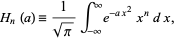(42)
|
which is simply given by
![H_n(a)=<span style=]() {(2I_n(a))/(sqrt(pi)) for n even; 0 for n odd. " src="http://mathworld.wolfram.com/images/equations/GaussianIntegral/NumberedEquation7.gif" style="height:64px; width:178px" /> |
(43)
|
The more general integral of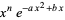 
has the following closed forms,
for integer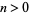 
(F. Pilolli, pers. comm.). For (45) and (46), ![a,b in C-<span style=]()
{0}" src="http://mathworld.wolfram.com/images/equations/GaussianIntegral/Inline132.gif" style="height:14px; width:78px" /> (the punctured plane), ![R[a]>0](http://mathworld.wolfram.com/images/equations/GaussianIntegral/Inline133.gif)
, and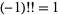 
. Here, 
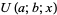is a confluent hypergeometric function of the second kind and 
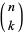is a binomial coefficient.
REFERENCES:
Guitton, E. "Démonstration de la formule." Nouv. Ann. Math. 65, 237-239, 1906.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Nicholas, C. B. and Yates, R. C. "The Probability Integral." Amer. Math. Monthly 57, 412-413, 1950.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 147-148, 1984.
Watson, G. N. "Theorems Stated by Ramanujan (IV): Theorems on Approximate Integration and Summation of Series." J. London Math. Soc. 3, 282-289, 1928.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
