q-Exponential Function
المؤلف:
Koekoek, R. and Swarttouw, R. F.
المصدر:
"The q-Gamma Function and the q-Binomial Coefficient." §0.3 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17
الجزء والصفحة:
...
27-8-2019
1856
q-Exponential Function
The exponential function has two different natural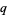 
-extensions, denoted 
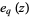and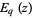 
. They are defined by
(Koekoek and Swarttouw 1998, p. 18), where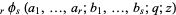 
is a q-hypergeometric function.
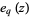has the special form
 |
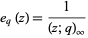(6)
|
for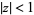 
.
The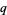 
-exponential functions are related to the q-cosine and q-sine by
REFERENCES:
Koekoek, R. and Swarttouw, R. F. "The q-Gamma Function and the q-Binomial Coefficient." §0.3 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 18-19, 1998.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
