q-Polygamma Function
المؤلف:
Borwein, J. M. and Borwein, P. B.
المصدر:
"Evaluation of Sums of Reciprocals of Fibonacci Sequences." §3.7 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley
الجزء والصفحة:
...
29-8-2019
1504
q-Polygamma Function
The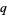 
-digamma function 
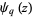, also denoted 
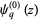, is defined as
 |
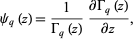(1)
|
where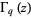 
is the q-gamma function. It is also given by the sum
 |
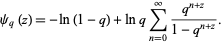(2)
|
The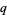 
-polygamma function 
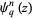(also denoted 
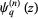) is defined by
 |
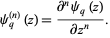(3)
|
It is implemented in the Wolfram Language as QPolyGamma[n, z, q], with the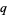 
-digamma function implemented as the special case QPolyGamma[z, q].
Certain classes of sums can be expressed in closed form using the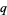 
-polygamma function, including
The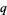 
-polygamma functions are related to the Lambert series
(Borwein and Borwein 1987, pp. 91 and 95).
An identity connecting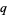 
-polygamma to elliptic functions is given by
![pi-i[psi_(phi^2)^((0))(1/2-(ipi)/(4lnphi))-psi_(phi^2)^((0))(1/2+(ipi)/(4lnphi))]
=-(lnphi)theta_2^2(phi^(-2)),](http://mathworld.wolfram.com/images/equations/q-PolygammaFunction/NumberedEquation4.gif) |
(9)
|
where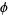 
is the golden ratio and 
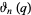is an Jacobi theta function.
REFERENCES:
Borwein, J. M. and Borwein, P. B. "Evaluation of Sums of Reciprocals of Fibonacci Sequences." §3.7 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 91-101, 1987.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
