Coulomb Wave Function
المؤلف:
Abramowitz, M. and Antosiewicz, H. A.
المصدر:
"Coulomb Wave Functions in the Transition Region." Phys. Rev. 96
الجزء والصفحة:
...
10-6-2019
2918
Coulomb Wave Function
A special case of the confluent hypergeometric function of the first kind. It gives the solution to the radial Schrödinger equation in the Coulomb potential (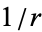
) of a point nucleus
![(d^2W)/(drho^2)+[1-(2eta)/rho-(L(L+1))/(rho^2)]W=0](http://mathworld.wolfram.com/images/equations/CoulombWaveFunction/NumberedEquation1.gif) |
(1)
|
(Abramowitz and Stegun 1972; Zwillinger 1997, p. 122). The complete solution is
 |
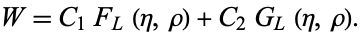(2)
|
The Coulomb function of the first kind is
 |
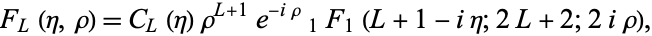(3)
|
where
 |
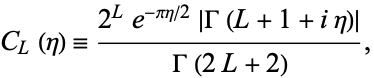(4)
|
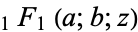is the confluent hypergeometric function of the first kind, 
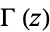is the gamma function, and the Coulomb function of the second kind is
![G_L(eta,rho)=(2eta)/(C_0^2(eta))F_L(eta,rho)[ln(2rho)+(q_L(eta))/(p_L(eta))]
+1/((2L+1)C_L(eta))rho^(-L)sum_(K=-L)^inftya_k^L(eta)rho^(K+L),](http://mathworld.wolfram.com/images/equations/CoulombWaveFunction/NumberedEquation5.gif) |
(5)
|
where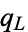 
, 
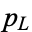, and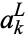 
are defined in Abramowitz and Stegun (1972, p. 538).
REFERENCES:
Abramowitz, M. and Antosiewicz, H. A. "Coulomb Wave Functions in the Transition Region." Phys. Rev. 96, 75-77, 1954.
Abramowitz, M. and Rabinowitz, P. "Evaluation of Coulomb Wave Functions along the Transition Line." Phys. Rev. 96, 77-79, 1954.
Abramowitz, M. and Stegun, I. A. (Eds.). "Coulomb Wave Functions." Ch. 14 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 537-544, 1972.
Biedenharn, L. C.; Gluckstern, R. L.; Hull, M. H. Jr.; and Breit, G. "Coulomb Wave Functions for Large Charges and Small Velocities." Phys. Rev. 97, 542-554, 1955.
Bloch, I.; Hull, M. H. Jr.; Broyles, A. A.; Bouricius, W. G.; Freeman, B. E.; and Breit, G. "Coulomb Functions for Reactions of Protons and Alpha-Particles with the Lighter Nuclei." Rev. Mod. Phys. 23, 147-182, 1951.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 631-633, 1953.
National Bureau of Standards. Tables of Coulomb Wave Functions, Vol. 1, Applied Math Series 17. Washington, DC: U.S. Government Printing Office, 1952.
Stegun, I. A. and Abramowitz, M. "Generation of Coulomb Wave Functions by Means of Recurrence Relations." Phys. Rev. 98, 1851-1852, 1955.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
