Shah Function
المؤلف:
Bracewell, R.
المصدر:
"The Sampling or Replicating Symbol m(x)." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill
الجزء والصفحة:
pp. 77-79 and 85
25-5-2019
2222
Shah Function
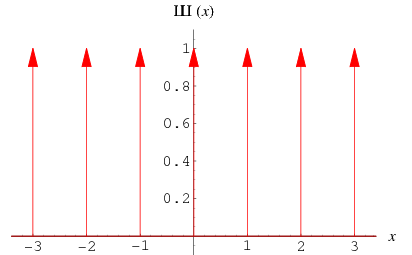
The shah function is defined by
where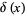 
is the delta function, so 
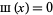for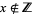 
(i.e., 
is not an integer). The shah function is also called the sampling symbol or replicating symbol (Bracewell 1999, p. 77), and is implemented in the Wolfram Language as DiracComb[x].
It obeys the identities
The shah function is normalized so that
 |
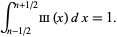(7)
|
The "sampling property" is
 |
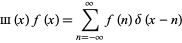(8)
|
and the "replicating property" is
 |
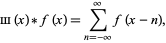(9)
|
where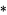 
denotes convolution.
The two-dimensional sampling function, sometimes called the bed-of-nails function, is given by
 |
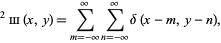(10)
|
which can be adjusted using a series of weights as
 |
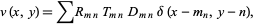(11)
|
where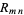 
is a reliability weight, 
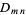is a density weight (weighting function), and 
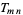is a taper. The two-dimensional shah function satisfies
 |
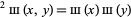(12)
|
(Bracewell 1999, p. 85).
REFERENCES:
Bracewell, R. "The Sampling or Replicating Symbol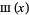 
." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 77-79 and 85, 1999.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
