Kennedy and Levins aspectual account

Kennedy and Levin propose that verbs of gradual change, that is, degree achievements and verbs with an incremental theme, be analyzed with the help of a certain three-place relation between individuals, degrees, and events that is based on a predicate increase and a gradable predicate constant G, as seen in (1a). The definition of increase, a four-place relation between gradable predicates, individuals, degrees, and events, is given in (1b).

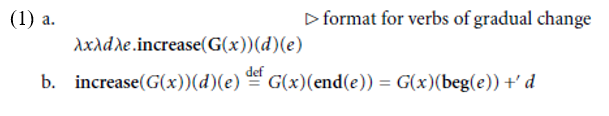
The gradable predicate constant G denotes a function that takes an individual x and a time t and yields the degree d to which G holds of x at t. This can be made more explicit with the help of the iota operator:¹

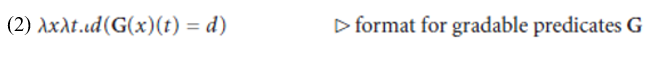
This, in turn, allows for a more explicit rendition of the formulas in (1)

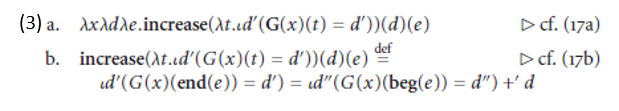
In prose, the definition in (3b) states that the degree to which the gradable predicate constant G holds of the individual x increases by the degree d in the event e just in case the degree to which G holds of x at the end of e is equal to the degree to which G holds of x at the beginning of e plus d. In other words, d, the so-called degree of change, signals the increase in the degree to which G holds of x in e. Note that the degree of change is always a positive degree.

Kennedy and Levin’s idea is that the relation in (3a) constitutes the common semantic element between degree achievements and verbs with an incremental theme – what differs is merely how G is instantiated. In each case, the meaning of the verb of gradual change is based on the meaning of a corresponding gradable adjective that instantiates G. As an illustration, two VPs containing a degree achievement are analyzed in (4) and (5), and two containing a verb with an incremental theme are represented in (6) and (7).

Notice that just as the meaning of shorten is based on the meaning of short, which denotes a function from individuals and times to (negative) degrees (short(x)(t) “the degree to which x is short at t”), the meaning of eat is based on the meaning of eaten, which likewise denotes a function from individuals and times to (negative) degrees (eaten(x)(t) “the degree to which x is eaten at t). Furthermore, given the definition in (19b), the formulas in (4b), (5b), (6b), and (7b) reduce to the following:

As Kennedy and Levin observe, the degree of change is not always syntactically expressed. In the case of degree achievements, it may be expressed by an explicit measure expression, as in (9a)² and (10a), but it may also remain implicit, as in (9b) and (10b), where it is existentially bound inside the VP.³

Kennedy and Levin also allow for the degree argument to remain free inside the VP (and possibly existentially bound from outside it), in contrast to the setup in (9b) and (10b), where it is existentially bound inside the VP. The degree argument remains free within the VP in the following variations on (9b) and (10b):

Observe that the event predicate representing the VP is quantized if the value of the degree argument is fixed within the VP:

For instance, consider the statements in (12). The event predicate in (9a) is quantized because any event in which the rope is lengthened by ten centimeters lacks a proper subevent in which it is lengthened by ten centimeters – in any proper subevent, it is at most lengthened by less than ten centimeters. Similarly, the event predicate in (11a) is quantized because any event in which the rope is lengthened by d-much lacks a proper subevent in which it is lengthened by d-much, where the value of d is implicit but fixed for the VP. In contrast, the event predicate in (9b) is cumulative – provided that it is nonunique – because the sum of any two events in which the rope is lengthened by some amount d is also an event in which the rope is lengthened by some (greater) amount d, where the value of d may vary with each event chosen. The reasoning behind the statements in (13) is analogous.

1 Kennedy and Levin do not make use of the iota operator. However, although a syntactic addition, the iota operator does not add anything on the semantic side that they are not already committed to. Once the logical language contains function symbols (e.g., G in 17b), issues of definedness arise, and so it is not the use of the iota operator in combination with function symbols that raises them.

2 A lingering worry is how the meaning of the term 10-cm for (by) ten centimeters in (25a) relates to the scale of length, which is closed at 0 and open at 1. Strictly speaking, positive degrees in this case should be intervals in [0, 1). For this to be intelligible, the length of ten centimeters should correspond to a positive degree in [0, 1), yet it is not evident which degree this should be. Although there may be a straightforward reply to this worry, it is at the same time easy to suspect that degrees in Kennedy and Levin’s account actually play a double role, as (i) indicators of degree of realization and (ii) measurements of particular extents. The question of degree addition is less problematic if the latter is the intended role for degrees. The resolution of this worry in the approach that I propose in section 8.3 consists in sharply distinguishing these two roles.

3 The superscript “atel” in (9b) and (10b) simply serves to mark the atelic interpretation of the VPs in question, thereby distinguishing them from those in (11a) and (11b) below, which are telic (and marked with “tel”).