A planar graph is. a graph that can be drawn in the plane without crossings - that is, so that no two edges intersect geometrically except at a vertex to which both are incident.

Any such drawing is a plane drawing. For convenience, we often use the abbreviation  plane graph for a plane drawing of a planar graph. For example, Fig. 1.1 shows three drawings of the planar graph K4, but only the second and third are plane graphs.

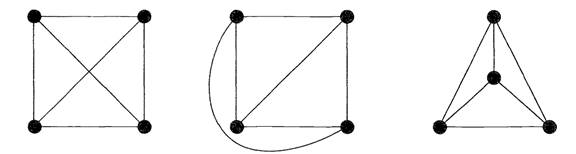
                                            Fig.  1.1

The right-hand drawing in Fig, 12.1 leads us to ask whether every planar graph can  be drawn in the plane so that each edge is represented by a straight line. Although  loops or multiple edges cannot be drawn as straight lines, it was proved independently  by K. Wagner in 1936 and I. Fa^`ry in 1948 that every simple planar graph can be drawn with straight lines; see Chartrand and Lesniak [2] for details.

Not all graphs are planar, as the following theorem shows:

THEOREM 1.1. k_3,3 and K₅ are non-planar.

Remark. We give two proofs of this result. The first one, presented here, is constructive. The second proof, which we give in Section, appears as a corollary of Euler's  formula.

Proof. Suppose first that K_3,3 is planar. Since K_3,3 has a cycle u → v →w → x →y →z →u of length 6, any plane drawing must contain this cycle drawn in the form of a hexagon, as in Fig. 1.2.

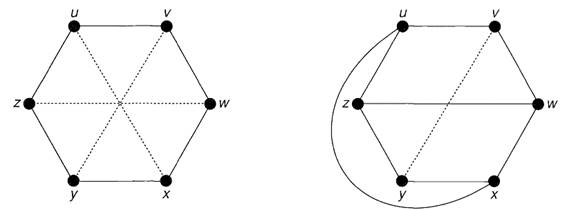
              Fig. 1.2                                                      Fig. 1.3

Now the edge wz must lie either wholly inside the hexagon or wholly outside it.  We deal with the case in which wz lies inside the hexagon - the other case is similar.

Since the edge ux must not cross the edge wz, it must lie outside the hexagon; the  situation is now as in Fig. 1.3. It is then impossible to draw the edge vy, as it wouldcross either ux or wz. This gives the required contradiction.

Now suppose that K$ is planar. Since K5 has a cycle v →w → x →y →z →vof  length 5, any plane drawing must contain this cycle drawn in the form of a pentagon, as  in Fig; 1.4.

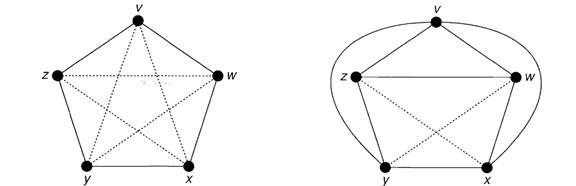
                       Fig. 1.4                                                      Fig. 1.5

Now the edge wz must lie either wholly inside the pentagon or wholly outside it. We  deal with the case in which wz lies inside the pentagon - the other case is similar. Since the edges vx and vy do not cross the edge wz, they must both lie outside the pentagon;  the situation is now as in Fig. 1.5. But the edge xz cannot cross the edge vy and so must lie inside the pentagon; similarly the edge wy must lie inside the pentagon, and  the edges wy and xz must then cross. This gives the required contradiction.

Note that every subgraph of a planar graph is planar, and that every graph with a  non-planar subgraph must be non-planar. It follows that any graph with k_3,3 or K₅ as asubgraph is non-planar. In fact, as we shall see, these two graphs are the 'building  blocks' for non-planar graphs, in the sense that every non-planar graph must 'contain' at least one of them.

THEOREM 1.2 (Kuratowski, 1930). A graph is planar if and only if it contains no  subgraph homeomorphic to K₅ or K_3,3.

The proof of Kuratowski's theorem is long and involved, and we omit it; see Bondy  and Murty [3] or Harary [4] for a proof. We shall, however, use Kuratowski's theorem to obtain another criterion for planarity. To do so, we first define a graph H to be contractible to K₅ or K_3,3 if we can obtain K₅ or K_3,3 by successively contracting edges of H. For example, the Petersen graph is contractible to K₅, as we can see by contracting  the five 'spokes' joining the inner and outer 5-cycles (see Fig. 1.6).

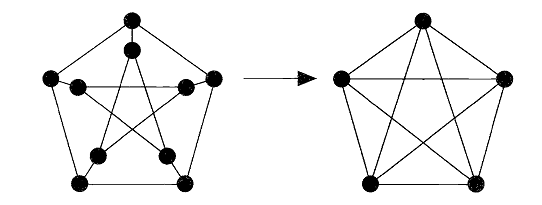
                                               Fig.1.6

THEOREM 1.3. A graph is planar if and only if it contains no subgraph  contractible to K₅ or K_3,3.

Sketch of proof. ← Assume first that the graph G is non-planar. Then, by Kuratowski's  theorem, G contains a subgraph H homeomorphic to K₅or k_3,3. On successively contracting edges of H that are incident td a vertex of degree 2, we see that H is contractible to K5 or k_3,3.

→Now assume that G contains a subgraph H contractible to K_3,3, and let the vertex  v of k_{3, 3} arise from contracting the subgraph H_v of H (see Fig. 1.7).

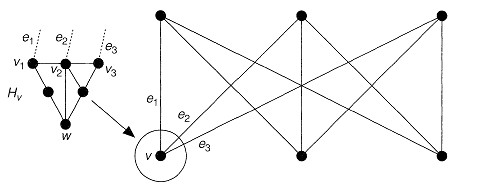
                                           Fig.1.7

The vertex v is incident in k_3,3 to three edges e₁, e₂ and e₃. When regarded as edges of H, these edges are incident to three (not necessarily distinct) vertices v₁, v₂ and v₃ of  Hv. If v₁, v₂ and V ₃ are distinct, then we can find a vertex w of H_v and three paths from  w to these vertices, intersecting only at w. (There is a similar construction if the vertices are not distinct, the paths degenerating in this case to single vertices.) It follows that we  can replace the subgraph H_v by a vertex w and three paths leading out of it. If this construction is carried out for each vertex of K_3,3, and the resulting paths joined up with  the corresponding edges of K_3,3, then the resulting subgraph is homeomorphic to K_3,3.

It follows from Kuratowski's theorem that G is non-planar (see Fig. 1.8).

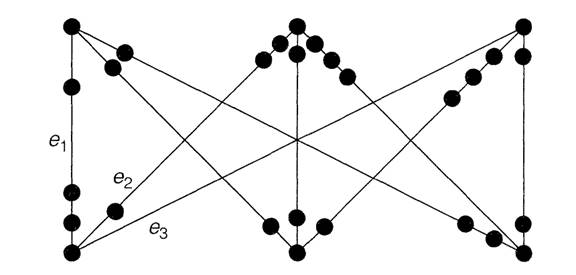
                                                  Fig.1.8

A similar argument can be carried out ifGcontainsasubgraphcontractibletok₅ . Herethedetailsaremorecomplicated,asthesubgraphweobtainbytheaboveprocess  Can be homeomorphic to either K₅ ork_3,3 ;see Chartrand and Lesniak  Weconcludethissectionbyintroducingthe'crossing-number'ofagraph.If we trytodrawk₅ork_3,3 on the plane, then there must be at least one crossing of edges, sincethesegraphsarenotplanar.However,wedonotneedmorethanonecrossing (seeFig.1.9),and wesaythatK₅and k_3,3 have crossing number1 .

Moregenerally,thecrossingnumbercr(G)ofagraphGistheminimumnumberofcrossingsthatcanoccurwhenGisdrawnintheplane.Thus,thecrossingnumber

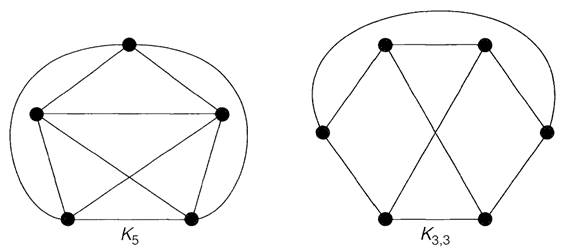
                                              Fig.1.9

Can be used to measure how 'unplanar ' G is .For example, the crossing number of any  planargraphis0,andcr(K₅)=cr(k _3,3)=1.Notethattheword'crossing 'always refers

To theintersection of just two edges; crossings of three or more edgesarenotpermitted.

1-Introduction to Graph Theory ,Fourth edition  ,Robin J. Wilson, British Library ,1996.page(60-64)

2-G. Chartrand and L. Lesniak, Graphs < & Digraphs, 2nd edn, Wadsworth & Brooks/Cole, 1986.

3- J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, American Elsevier, 1979.

4- F. Harary, Graph Theory, Addison-Wesley, 1969.

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength