
آخر المواضيع المضافة


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 23-8-2016
Date: 11-8-2016
Date: 11-8-2016
|
Momentum Perturbation
A particle of mass m moves in one dimension according to the Hamiltonian
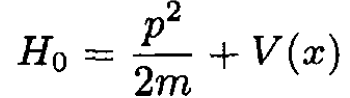 (1)
(1)
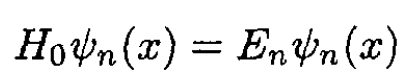 (2)
(2)
All eigenfunctions ѱn(x) and eigenvalues En are known. Suppose we add a term to the Hamiltonian, where λ and m are constants and p is the momentum operator:
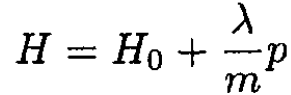 (3)
(3)
Derive an expression for the eigenvalues and eigenstates of the new Hamiltonian H.
SOLUTION
The first step is to rewrite the Hamiltonian by completing the square on the momentum operator:
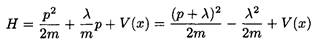 (1)
(1)
The constant just shifts the zero of the momentum operator. The rewritten Hamiltonian in (1) suggests the perturbed eigenstates:
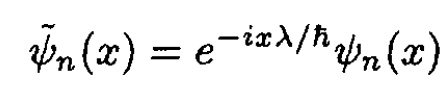 (2)
(2)
The action of the displaced momentum operator p + λ on the new eigenstates is
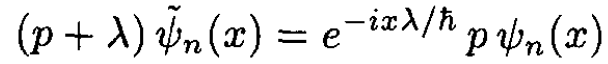 (3)
(3)
so the Hamiltonian gives
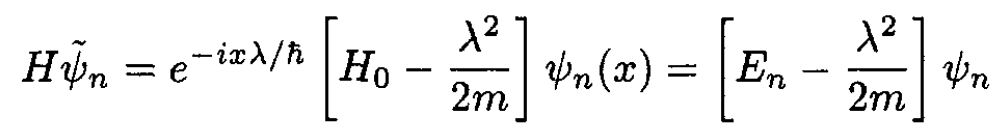 (4)
(4)
and the eigenvalues are simply
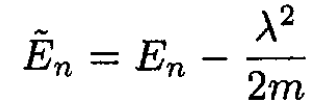 (5)
(5)



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق باحث يتطرّق إلى استراتيجية كرسي اليونسكو في دراسات منع الإبادة الجماعية في العالم الإسلامي
|
|
|