Rational Approximation

If 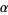 is any number 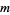and  and 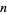 are integers, then there is a rational number  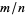for which

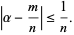(1)

If 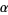 is irrational and  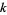is any whole number, there is a fraction  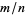with 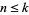 and for which

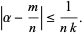(2)

Furthermore, there are an infinite number of fractions 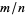 for which

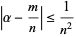(3)

(Hilbert and Cohn-Vossen 1999, pp. 40-44).

Hurwitz has shown that for an irrational number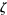 

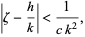(4)

there are infinitely rational numbers 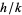 if 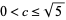, but if 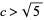, there are some  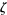for which this approximation holds for only finitely many .

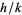REFERENCES:

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 41, 1999.