


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-8-2018
Date: 12-10-2018
Date: 18-9-2019
|
The largest value of a set, function, etc. The maximum value of a set of elements 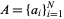 is denoted
is denoted 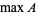 or
or 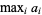 , and is equal to the last element of a sorted (i.e., ordered) version of
, and is equal to the last element of a sorted (i.e., ordered) version of 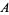 . For example, given the set
. For example, given the set 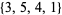 , the sorted version is
, the sorted version is 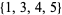 , so the maximum is 5. The maximum and minimum are the simplest order statistics.
, so the maximum is 5. The maximum and minimum are the simplest order statistics.
The maximum value of a variable  is commonly denoted
is commonly denoted 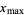 (Strang 1988, pp. 286-287 and 301-303) or
(Strang 1988, pp. 286-287 and 301-303) or 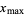 (Golub and Van Loan 1996, p. 74). In this work, the convention
(Golub and Van Loan 1996, p. 74). In this work, the convention 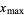 is used.
is used.
The maximum of a set of elements is implemented in the Wolfram Language as Max[list] and satisfies the identities
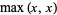 |
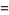 |
 |
(1) |
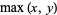 |
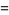 |
 |
(2) |
Definite integrals include
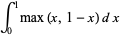 |
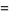 |
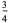 |
(3) |
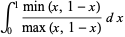 |
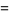 |
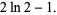 |
(4) |
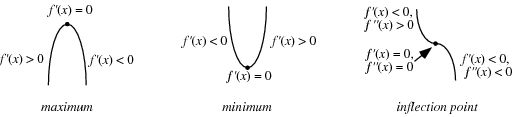
A continuous function may assume a maximum at a single point or may have maxima at a number of points. A global maximum of a function is the largest value in the entire range of the function, and a local maximum is the largest value in some local neighborhood.
For a function 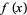 which is continuous at a point
which is continuous at a point 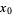 , a necessary but not sufficient condition for
, a necessary but not sufficient condition for 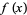 to have a local maximum at
to have a local maximum at 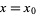 is that
is that 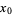 be a critical point (i.e.,
be a critical point (i.e., 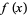 is either not differentiable at
is either not differentiable at 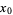 or
or 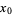 is a stationary point, in which case
is a stationary point, in which case 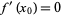 ).
).
The first derivative test can be applied to continuous functions to distinguish maxima from minima. For twice differentiable functions of one variable, 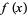 , or of two variables,
, or of two variables, 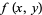 , the second derivative test can sometimes also identify the nature of an extremum. For a function
, the second derivative test can sometimes also identify the nature of an extremum. For a function 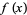 , the extremum test succeeds under more general conditions than the second derivative test.
, the extremum test succeeds under more general conditions than the second derivative test.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Golub, G. and Van Loan, C. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
Niven, I. Maxima and Minima without Calculus. Washington, DC: Math. Assoc. Amer., 1982.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Minimization or Maximization of Functions." Ch. 10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 387-448, 1992.
Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.
Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|