The example 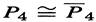suggests a family of graph problems.

1.1. Definition.

A graph is self-complementary if it is isomorphic to its complement. A decomposition of a graph is a list of subgraphs such that

each edge appears in exactly one subgraph in the list.

An n-vertex graph H is self-complementary if and only if K_n has a decomposition consisting of two copies of H.

1.2 Example.

We can decompose K5 into two 5-cycles, and thus the 5-cycle is self-complementary. Any n-vertex graph and its complement decompose Kn.

Also K_l,n-l and K_n-l. decompose K_n, even though one of these subgraphs omits a vertex. On the right below we show a decomposition of K₄

using three copies consider graph decompositions. .

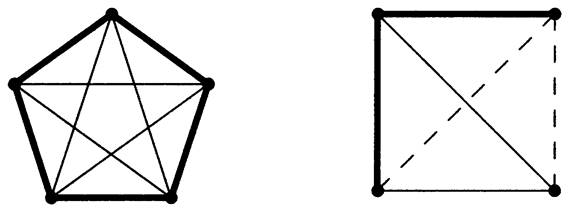
1.3 Example.

The question of which complete graphs decompose into copies of K₃ is a fundamental question in the theory of combinatorial designs.

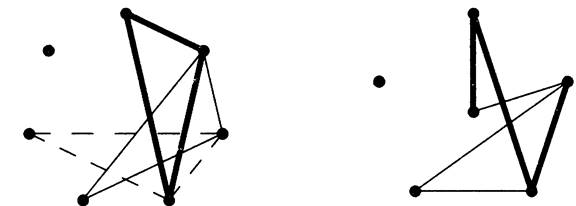
On the left below we suggest such a decomposition for K₇. Rotating the triangle through seven positions uses each edge exactly once.

On the right we suggest a decomposition of K₆ into copies of P₄. Placing one vertex in the center groups the edges into three types: the outer 5-cycle, the inner (crossing) 5-cycle on those vertices, and the edges involving the central vertex. Each 4-vertex path in the decomposition uses one edge of each type; we rotate the picture to get the next path.

We referred to a copy of K₃ as a triangle. Short names for graphs that arise frequently in structural discussions can be convenient.

1.4. Definition.

The Petersen graph is the simple graph whose vertices are the 2-element subsets of a 5-element set and whose edges are the pairs

of disjoint 2-element subsets.

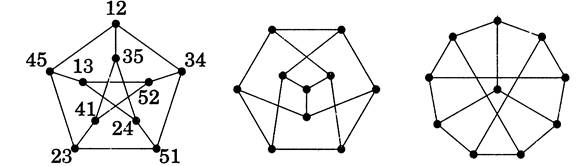
We have drawn the Petersen graph in three ways above. It is a useful example so often that an entire book was devoted to it (Holton-Sheell an [I993]).

Its properties follow from the statement of its adjacency relation that we have used as the definition.

1.5. Proposition.

If two vertices are nonadjacent in the Petersen graph, then they have exactly one common neighbor.

proof.

Non adjacent vertices are 2-sets sharing one element; their union S has size 3. A vertex adjacent to both IS a 2-set disjoint from both. Since the 2-sets

are chosen from {1, 2, 3,4, 5}, there is exactly one 2-set disjoint from S.

1.6 Definition.

The girth of a graph with a cycle is the length of its shortest cycle. A graph with no cycle has infinite girth.

1.7 Definition.

An automorphism of G is an isomorphism from G to G. A graph G is vertex-transitive if for every pair u, v ϵ V (G) there is an automorphism that maps u to v.

The automorphisms of G are the permutations of V (G) that can be applied to both the rows and the columns of A(G) without changing A(G).

Introduction to Graph Theory Second Edition, Douglas B. West , Indian Reprint, 2002,page(8.10)

​

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength