Connectedness

المؤلف:  Jean-Claude Fournier

المصدر:  Graph Theory and Applications

الجزء والصفحة:  35-36

28-7-2016

1600

A G graph is said to be connected if any two vertices of this graph are linked by a path in G. Otherwise, the graph is a disconnected graph.

  The connected components of a graph G are the maximal connected induced subgraphs of G. Maximal means here that the subgraph mentioned is not itself a proper subgraph, that is with strictly fewer vertices, of a connected subgraph of G. Obviously, a graph is connected if and only if it has only  one connected component.

  We verify that the connected components of a graph are subgraphs pairwise disjoint, that is having pairwise no common vertices and no common edges. It defines the decomposition into connected components of the graph (see Figure 1.1 for an example). This decomposition is unique.

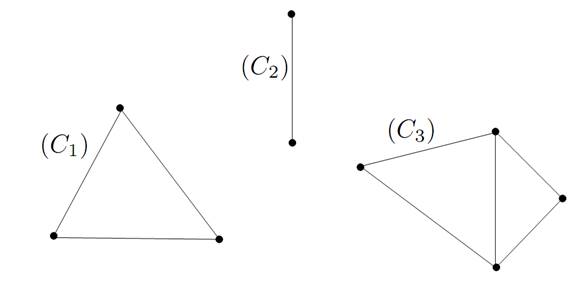
Figure 1.1. A disconnected graph and its three connected components: C₁,C₂, C₃

                  It is also possible to define in algebraic language the connected components of a graph G =(X,E) as the subgraphs induced by equivalence classes over X, defined by the relation: the vertices x and y are linked by a path. This binary relation is in fact an equivalence relation on the set X  (reflexive, symmetric and transitive).

To finish connectedness, let us just mention the following proposition:

If a graph possesses a spanning subgraph which is connected, it is itself connected. This proposition is one of many small propositions which are often not proved or even stated. Nevertheless it is useful for a beginner in graph theory to practice by proving them rigorously at least once. If we can do this easily, then all is well, at least so far into the theory. If we do not succeed, we should go back over the preceding pages or maybe rethink our personal logic.

Graph Theory  and Applications ,Jean-Claude Fournier, WILEY, page(35-36)