1. What Is a Graph?

How can we lay cable at minimum cost to make every telephone reachable  from every other? What is the fastest route from the national capital to each  state capital? How can n jobs be filled by n people with maximum total utility?  What is the maximum flow per unit time  from source to sink in a network of  pipes? How many layers does a computer chip need so that wires in the same  layer don't cross?

 How can the season of a sports league be scheduled into the  minimum number of weeks? In what order should a traveling salesman visit  cities to minimize travel time? Can we color the regions of every map using  four colors so that neighboring regions receive different colors?  These and many other practical problems involve graph theory. In this  book, we develop the theory of graphs and apply it to such problems. Our  starting point assumes the mathematical background in Appendix A, where  basic objects and language of mathematics are discusse

THE DEFINITION

The problem that is often sard to have been the birth of graph theory will  suggest our basic definition of a graph.

1.1.1. Example. The Konigsberg Bridge Problem. The city of Konigsberg was  located on the Pregel river in Prussia. The city occupied two islands plus ar-

eas on both banks. These regions were linked by seven bridges as shown on  the left below. The citizens wondered whether they could leave home, cross ev-

ery bridge exactly once, and return home. The problem reduces to traversing  the figure on the right, with heavy dots representing land masses and curves

representing bridges.

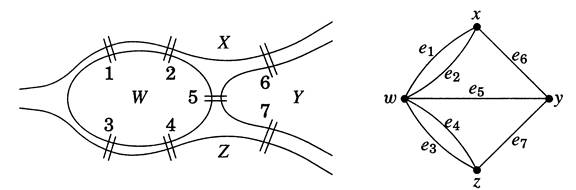
The model on the right makes it easy to argue that the desired traversal  does not exist. Each time we enter and leave a land mass, we use two bridges

ending at it. We can also pair the first bridge with the last bridge on the land  mass where we begin and end. Thus existence of the desired traversal requires

that each land mass be involved in an even number of bridges. This necessary  condition did not hold in Konigsberg. ' .

­The Konigsberg Bridge Problem becomes more interesting when we show  in Section of(Paths, Cycles, and Trails ) which configurations have traversals. Meanwhile, the problem

suggests a general model for discussing such questions.

1.1.2. Definition. A graph G IT is a triple consisting of a vertex set V(G), an  edge set E(G), and a relation that associates with each edge two vertices

(not necessarily distinct) called its endpoints.  We draw a graph on paper by placing each vertex at a point and representing each edge by a curve joining the locations of its endpoints.

1.1.3. Example.

In the graph in Example 1.1.1, the vertex set is {x, y, z, w},  the edge set is {e₁, e₂, e₃, e₄, e_s, e₆, e₇}, and the assignment of endpoints to edges

can be read from the picture. Note that edges el and e₂ have the same endpoints, as' do e₃ and e₄. Also, if we had a bridge over an inlet, then

its ends would be in the same land mass,  and we would draw it as a curve with both ends at the same point. We have  appropriate terms for

 these types of edges in graphs.

1.1.4   Definition. A loop is an edge whose endpoints are equal. Multiple edges are edges having the same pair of endpoints.

A simple graph is a graph having no loops or multiple edges. We specify a simple graph by its vertex set and edge set,

 treating the edge set as a set of unordered pairs of vertices and writing e = uv (or e = vu) for an edge e with endpoints u and u.

When u and v are the endpoints of an edge, they are adjacent and are neighbors. We write u↔ v for “w is adjacent to v”.

 In many important applications, loops and multiple edges do not arise, and we restrict our attention to simple graphs. In this case an edge is determined by its endpoints, so we can name the edge by its endpoints, as stated in Definition  1.1.4. Thus in a simple graph we view an edge as an unordered pair of vertices and can ignore the formality of the relation associating endpoints to edges. This  book emphasizes simple graphs.

1.1.5. Example. On the left below are two drawings of a simple graph. The  vertex set is {u, v, w, x, y}, and the edge set is {uv, uw, ux, vx, vw, xw, xy}.

The terms "vertex" and "edge" arise from solid geometry. A cube has vertices and edges, and these form the vertex set and edge set of a graph. It is drawn on the right below, omitting the names of vertices and edges.

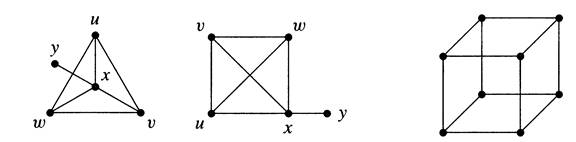
A graph is finite if its vertex set and edge set are finite. We adopt the convention that every graph mentioned in this book is finite, unless explicitly constructed otherwise.

­1.1.6. Remark. The null graph is the graph whose vertex set and edge set are empty. Extending general theorems to the null graph introduces unnecessary distractions, so we ignore it. All statements and exercises should be  considered only for graphs with a nonempty set of vertices.

_____________________________________________________________________________________________

Introduction to Graph Theory Second Edition, Douglas B. West , Indian Reprint, 2002,page(1.3)

مواضيع ذات صلة

Minimum Spanning Tree

Maximum Leaf Number

Lobster Graph

Labeled Tree

Internal Path Length

Red-Black Tree

Pseudotree

Pseudoforest

Prüfer Code

Planted Tree

Planted Planar Tree

Graph Strength