Box Fractal
المؤلف:
Sloane, N. J. A
المصدر:
Sequences A000351/M3937 and A113209 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
13-9-2021
1800
Box Fractal
The box fractal is a fractal also called the anticross-stitch curve which can be constructed using string rewriting beginning with a cell [1] and iterating the rules
![<span style=]() {0->[0 0 0; 0 0 0; 0 0 0],1->[1 0 1; 0 1 0; 1 0 1]}. " src="https://mathworld.wolfram.com/images/equations/BoxFractal/NumberedEquation1.gif" style="height:54px; width:192px" /> |
(1)
|
An outline of the box fractal can encoded as a Lindenmayer system with initial string "F-F-F-F", string rewriting rule "F" -> "F-F+F+F-F", and angle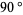 
(J. Updike, pers. comm., Oct. 26, 2004).
Let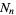 
be the number of black boxes, 
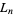the length of a side of a white box, and 
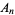the fractional area of black boxes after the 
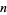th iteration.
The sequence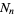 
is then 1, 5, 25, 125, 625, 3125, 15625, ... (OEIS A000351). The capacity dimension is therefore
(OEIS A113209).
REFERENCES:
Sloane, N. J. A. Sequences A000351/M3937 and A113209 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
