Braid
المؤلف:
Artin, E.
المصدر:
"The Theory of Braids." Amer. Sci. 38,
الجزء والصفحة:
...
6-6-2021
1981
Braid
A braid is an intertwining of some number of strings attached to top and bottom "bars" such that each string never "turns back up." In other words, the path of each string in a braid could be traced out by a falling object if acted upon only by gravity and horizontal forces. A given braid may be assigned a symbol known as a braid word that uniquely identifies it (although equivalent braids may have more than one possible representations). For example,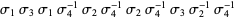 
is a braid word for the braid illustrated above.
If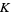 
is a knot and
where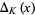 
is the Alexander polynomial of 
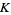, then 
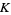cannot be represented as a closed 3-braid. Also, if
then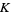 
cannot be represented as a closed 4-braid (Jones 1985).
REFERENCES:
Artin, E. "The Theory of Braids." Amer. Sci. 38, 112-119, 1950.
Christy, J. "Braids." http://library.wolfram.com/infocenter/MathSource/813/.
Jones, V. "A Polynomial Invariant for Knots via von Neumann Algebras." Bull. Amer. Math. Soc. 12, 103-111, 1985.
Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
