


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2021
Date: 23-12-2021
Date: 31-12-2021
|
A lattice 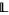 is locally bounded if and only if each of its finitely generated sublattices is bounded.
is locally bounded if and only if each of its finitely generated sublattices is bounded.
Every locally bounded lattice is locally subbounded, and every locally bounded lattice 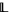 has a bounded hyperfinite extension in any nonstandard enlargement
has a bounded hyperfinite extension in any nonstandard enlargement 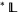 . This latter nonstandard property characterizes locally subbounded lattices.
. This latter nonstandard property characterizes locally subbounded lattices.
A locally bounded lattice is locally tight if and only if each of its hyperfinitely generated extensions is internally tight. One can also prove the following result, using nonstandard characterizations of these notions: Let 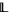 be a locally finite lattice with at least one strictly increasing meet endomorphism and at least one strictly decreasing join endomorphism. If
be a locally finite lattice with at least one strictly increasing meet endomorphism and at least one strictly decreasing join endomorphism. If 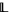 is locally tight, then it is bounded.
is locally tight, then it is bounded.
REFERENCES:
Grätzer, G. Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|