


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-7-2021
Date: 23-7-2021
Date: 31-7-2021
|
The tangent plane to a surface at a point 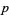 is the tangent space at
is the tangent space at 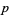 (after translating to the origin). The elements of the tangent space are called tangent vectors, and they are closed under addition and scalar multiplication. In particular, the tangent space is a vector space.
(after translating to the origin). The elements of the tangent space are called tangent vectors, and they are closed under addition and scalar multiplication. In particular, the tangent space is a vector space.
Any submanifold of Euclidean space, and more generally any submanifold of an abstract manifold, has a tangent space at each point. The collection of tangent spaces 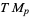 to
to 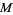 forms the tangent bundle
forms the tangent bundle  . A vector field assigns to every point
. A vector field assigns to every point 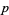 a tangent vector in the tangent space at
a tangent vector in the tangent space at 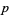 .
.
There are two ways of defining a submanifold, and each way gives rise to a different way of defining the tangent space. The first way uses a parameterization, and the second way uses a system of equations.
Suppose that 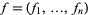 is a local parameterization of a submanifold
is a local parameterization of a submanifold 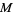 in Euclidean space
in Euclidean space 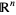 . Say,
. Say,
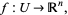 |
(1) |
where 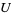 is the open unit ball in
is the open unit ball in 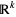 , and
, and 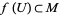 . At the point
. At the point 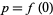 , the tangent space is the image of the Jacobian of
, the tangent space is the image of the Jacobian of 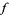 , as a linear transformation from
, as a linear transformation from 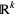 to
to 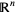 . For example, consider the unit sphere
. For example, consider the unit sphere
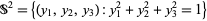 |
(2) |
in 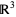 . Then the function (with the domain
. Then the function (with the domain 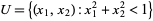 )
)
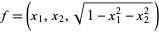 |
(3) |
parameterizes a neighborhood of the north pole. Its Jacobian at 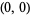 is given by the matrix
is given by the matrix
![[1 0; 0 1; 0 0]](https://mathworld.wolfram.com/images/equations/SubmanifoldTangentSpace/NumberedEquation4.gif) |
(4) |
whose image is the tangent space at 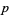 ,
,
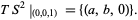 |
(5) |
An alternative description of a submanifold 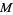 as the set of solutions to a system of equations leads to another description of tangent vectors. Consider a submanifold
as the set of solutions to a system of equations leads to another description of tangent vectors. Consider a submanifold 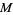 which is the set of solutions to the system of equations
which is the set of solutions to the system of equations
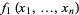 |
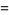 |
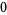 |
(6) |
 |
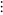 |
 |
(7) |
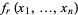 |
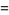 |
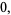 |
(8) |
where 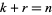 and the Jacobian of
and the Jacobian of 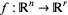 , with
, with 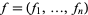 , has rank
, has rank 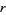 at the solutions
at the solutions 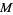 to
to 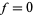 . A tangent vector
. A tangent vector 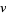 at a solution
at a solution 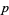 is an infinitesimal solution to the above equations (at
is an infinitesimal solution to the above equations (at 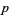 ). The tangent vector
). The tangent vector 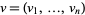 is a solution of the derivative (linearization) of
is a solution of the derivative (linearization) of 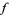 , i.e., it is in the null space of the Jacobian.
, i.e., it is in the null space of the Jacobian.
Consider this method in the recomputation the tangent space of the sphere at the north pole. The sphere is two-dimensional and is described as the solution to single equation (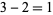 )
) 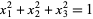 . Set
. Set 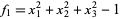 . We want to compute the tangent space at the solution
. We want to compute the tangent space at the solution 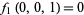 (at the north pole). The Jacobian at this point is the
(at the north pole). The Jacobian at this point is the 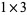 matrix
matrix ![[0,0,2]](https://mathworld.wolfram.com/images/equations/SubmanifoldTangentSpace/Inline49.gif) , and its null space is the tangent space
, and its null space is the tangent space
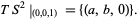 |
(9) |
It appears that the tangent space depends either on the choice of parametrization, or on the choice of system of equations. Because the Jacobian of a composition of functions obeys the chain rule, the tangent space is well-defined. Note that the Jacobian of a diffeomorphism is an invertible linear map, and these correspond to the ways the equations can be changed. The basic facts from linear algebra used to show that the tangent space is well-defined are the following.
1. If 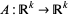 is invertible, then the image of
is invertible, then the image of 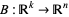 is the same as the image of
is the same as the image of 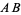 .
.
2. If 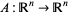 is invertible, then the null space of
is invertible, then the null space of 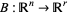 is the same as the null space of
is the same as the null space of 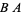 . More precisely,
. More precisely, 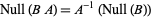 .
.
These techniques work in any dimension. In addition, they generalize to submanifolds of an abstract manifold, because tangent vectors depend on local properties. In particular, the tangent space can be computed in any coordinate chart, because any change in coordinate chart corresponds to a diffeomorphism in Euclidean space.
The tangent space can give some geometric insight to higher-dimensional phenomena. For example, to compute the tangent space to the torus (donut) 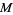 in
in 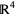 (which is a flat manifold), note that it can be parametrized, by
(which is a flat manifold), note that it can be parametrized, by
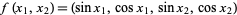 |
(10) |
with domain 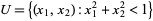 , near the point
, near the point 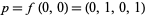 . Its Jacobian at
. Its Jacobian at 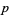 is the matrix
is the matrix
![[1 0; 0 0; 0 1; 0 0],](https://mathworld.wolfram.com/images/equations/SubmanifoldTangentSpace/NumberedEquation8.gif) |
(11) |
whose image is the tangent space 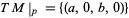 .
.
Alternatively, 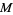 is the set of solutions to equations
is the set of solutions to equations
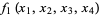 |
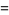 |
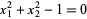 |
(12) |
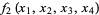 |
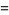 |
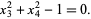 |
(13) |
The Jacobian at the solution 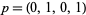 is the matrix
is the matrix
![[0 2 0 0; 0 0 0 2],](https://mathworld.wolfram.com/images/equations/SubmanifoldTangentSpace/NumberedEquation9.gif) |
(14) |
whose null space is the tangent space 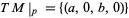 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|