Multidimensional Point Process

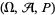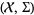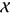A multidimensional point process is a measurable function from a probability space  into  where  is the set of all finite or countable subsets of  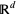not containing an accumulation point and where  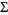is the sigma-algebra generated over  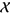by the sets

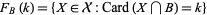for all bounded Borel subsets 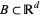. Here,  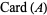denotes the cardinality or order of the set .

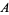A multidimensional point process is sometimes abbreviated MPP, though care should be exhibited not to confuse the notion with that of a marked point process.

Despite a number of apparent differences, one can show that multidimensional point processes are a special case of a random closed set on 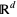 (Baudin 1984).

REFERENCES:

Baudin, M. "Multidimensional Point Processes and Random Closed Sets." J. Appl. Prob. 21, 173-178, 1984.

Matheron, G. Random Sets and Integral Geometry. New York: Wiley, 1975.