A mass on a vertical spring

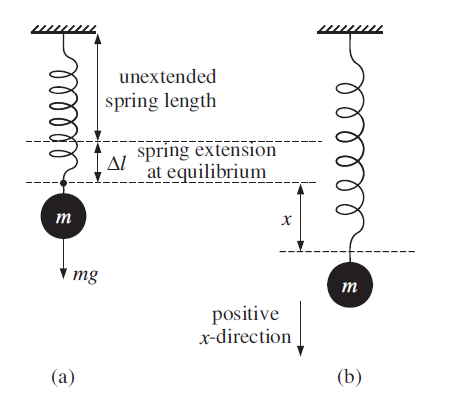
Figure 1.1 An oscillating mass on a vertical spring. (a) The mass at its equilibrium position. (b) The mass displaced by a distance x from its equilibrium position.
If we suspend a mass from a vertical spring, as shown in Figure 1.1, we have gravity also acting on the mass. When the mass is initially attached to the spring, the length of the spring increases by an amount Δl. Taking displacements in the downward direction as positive, the resultant force on the mass is equal to the gravitational force minus the force exerted upwards by the spring, i.e. the resultant force is given by mg − kΔl. The resultant force is equal to zero when the mass is at its equilibrium position. Hence

kΔl = mg.
When the mass is displaced downwards by an amount x, the resultant force is given by

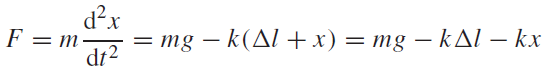
i.e.

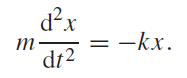
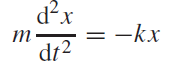..........(1)

Perhaps not surprisingly, this result is identical to the equation of motion (1) of the horizontal spring: we simply need to measure displacements from the equilibrium position of the mass.