Lucas,s Theorem
المؤلف:
Brent, R. P.
المصدر:
"On Computing Factors of Cyclotomic Polynomials." Math. Comput. 61
الجزء والصفحة:
...
14-9-2020
1386
Lucas's Theorem
Lucas's theorem states that if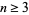 
be a squarefree integer and 
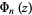a cyclotomic polynomial, then
 |
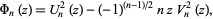(1)
|
where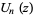 
and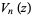 
are integer polynomials of degree 
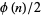and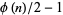 
, respectively. This identity can be expressed as
![<span style=]() {Phi_n((-1)^((n-1)/2)z)=C_n^2(z)-nzD_n^2(z) for n odd; Phi_(n/2)(-z^2)=C_n^2(z)-nzD_n^2(z) n=4k+2; -Phi_1(-z^2)=C_2^2(z)-2zD_2^2(z) for n=2, " src="https://mathworld.wolfram.com/images/equations/LucassTheorem/NumberedEquation2.gif" style="height:80px; width:299px" /> |
(2)
|
with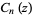 
and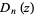 
symmetric polynomials. The following table gives the first few 
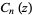and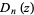 
s (Riesel 1994, pp. 443-456).
REFERENCES:
Brent, R. P. "On Computing Factors of Cyclotomic Polynomials." Math. Comput. 61, 131-149, 1993.
Kraitchik, M. Recherches sue la théorie des nombres, tome I. Paris: Gauthier-Villars, pp. 126-128, 1924.
Riesel, H. "Lucas's Formula for Cyclotomic Polynomials." In tables at end of Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 443-456, 1994.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
