


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 5-9-2020
Date: 16-8-2020
Date: 3-3-2016
|
Stellar magnitudes
Certainly, in the optical region of the spectrum, it is not normal practice to measure stellar fluxes
absolutely. A preliminary description was given of the magnitude scale as proposed
by Hipparchus whereby the brightnesses of stars are compared in a relative way. This scheme has
perpetuated through the subsequent centuries.
In the late 18th and 19th centuries, several astronomers performed experiments to see how the
magnitude scale was related to the amount of energy received. It appeared that a given difference
in magnitude, at any point in the magnitude scale, corresponded to a ratio of the brightnesses which
was virtually constant. Following his studies of apparent brightness variations of asteroids resulting
from their changes in distance from the Earth, in 1856 Pogson proposed that the value of the ratio,
corresponding to a magnitude difference of five, should be 100. Thus, the ratio of two stellar
brightnesses, B1 and B2, can be related to their magnitudes, m1 and m2, by the equation
B1/B2 = 2·512−(m1−m2) (1)
since (2·512)5 equals 100. This is known as Pogson’s equation. The negative sign before the bracketed
exponent reflects the fact that magnitude values increase as the brightness falls. By taking logarithms
of equation (1), we obtain
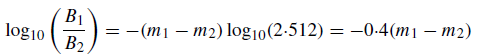
or
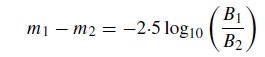 (2)
(2)
thus showing that the early tabulated magnitudes were proportional to the logarithm of the stellar brightness. This fact is a result of the way that the eye responds, a fact embodied in theWeber–Fechner law. This states that the smallest recognizable change in stimulus is proportional to the already existing stimulus, giving rise to the notion that our senses to stimuli are logarithmic. Hence, Pogson’s equation is normally written in one of the three following ways:
B1/B2 = 2·512−(m1−m2)
m1 − m2 = −2·5 log10(B1/B2)
log10(B1/B2)= −0·4(m1 − m2). (3)
More generally, Pogson’s equation in the style of equation (2) can be presented in a simplified form as
m = k − 2·5 log10 B (4)
where m is the magnitude of the star, B its apparent brightness and k some constant. The value of k is chosen conveniently by assigning a magnitude to one particular star such as α Lyr, or set of stars, thus fixing the zero point to that magnitude scale. It should also be noted that the numerical coefficient of 2·5 in equation (2) is exact and is not a rounded value of 2·512 from equation (1).



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|