


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-12-2019
Date: 30-12-2020
Date: 12-12-2020
|
The group of an elliptic curve which has been transformed to the form
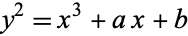 |
is the set of 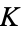 -rational points, including the single point at infinity. The group law (addition) is defined as follows: Take 2
-rational points, including the single point at infinity. The group law (addition) is defined as follows: Take 2 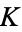 -rational points
-rational points 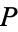 and
and 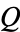 . Now 'draw' a straight line through them and compute the third point of intersection
. Now 'draw' a straight line through them and compute the third point of intersection 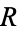 (also a
(also a 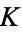 -rational point). Then
-rational point). Then
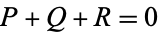 |
gives the identity point at infinity. Now find the inverse of 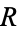 , which can be done by setting
, which can be done by setting 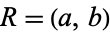 giving
giving 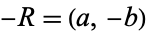 .
.
This remarkable result is only a special case of a more general procedure. Essentially, the reason is that this type of elliptic curve has a single point at infinity which is an inflection point (the line at infinity meets the curve at a single point at infinity, so it must be an intersection of multiplicity three).



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|