


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-1-2020
Date: 27-1-2020
Date: 13-12-2020
|
Quinn et al. (2007) investigated a class of 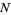 coupled oscillators whose bifurcation phase offset had a conjectured asymptotic behavior of
coupled oscillators whose bifurcation phase offset had a conjectured asymptotic behavior of 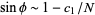 , with an experimental estimate for the constant
, with an experimental estimate for the constant 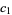 as
as 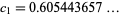 (OEIS A131329). Rather amazingly, Bailey et al. (2007) were able to find a closed form for
(OEIS A131329). Rather amazingly, Bailey et al. (2007) were able to find a closed form for 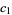 as the unique root of
as the unique root of 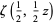 in the interval
in the interval ![[0,2]](https://mathworld.wolfram.com/images/equations/QRSConstant/Inline7.gif) , where
, where 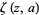 is a Hurwitz zeta function.
is a Hurwitz zeta function.
A related constant conjectured by Quinn et al. (2007) to exist was defined in terms of
![S(N,a)=sum_(i=1)^N[1-a^2(1-(2i-2)/(N-1))^2]^(-3/2)](https://mathworld.wolfram.com/images/equations/QRSConstant/NumberedEquation1.gif) |
(1) |
and given by
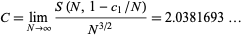 |
(2) |
(OEIS A131330). Even more amazingly, the exact value of this constant was also found by Bailey et al. (2007) without full proof, but with enough to indicate that such a proof could in principle be constructed, to have the exact value
![C=1/4zeta(3/2,1/2c_1)].](https://mathworld.wolfram.com/images/equations/QRSConstant/NumberedEquation3.gif) |
(3) |
REFERENCES:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "Resolution of the Quinn-Rand-Strogatz Constant of Nonlinear Physics." Preprint. June 4, 2007. https://users.cs.dal.ca/~jborwein/QRS.pdf.
Quinn, D. ; Rand, R.; and Strogatz, S. "Singular Unlocking Transition in the Winfree Model of Coupled Oscillators." Phys. Rev. E 75, 036218-1-10, 2007.
Sloane, N. J. A. Sequences A131329 and A131330 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|