
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-10-2019
Date: 4-3-2020
Date: 31-10-2019
|
Let 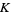 be a number field and let
be a number field and let 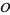 be an order in
be an order in 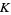 . Then the set of equivalence classes of invertible fractional ideals of
. Then the set of equivalence classes of invertible fractional ideals of 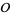 forms a multiplicative Abelian group called the Picard group of
forms a multiplicative Abelian group called the Picard group of 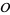 .
.
If 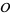 is a maximal order, i.e., the ring of integers of
is a maximal order, i.e., the ring of integers of 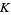 , then every fractional ideal of
, then every fractional ideal of 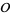 is invertible and the Picard group of
is invertible and the Picard group of 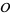 is the class group of
is the class group of 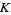 . The order of the Picard group of
. The order of the Picard group of 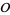 is sometimes called the class number of
is sometimes called the class number of 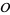 . If
. If 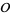 is maximal, then the order of the Picard group is equal to the class number of
is maximal, then the order of the Picard group is equal to the class number of 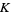 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|