


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-8-2019
Date: 31-7-2019
Date: 28-4-2019
|
The Poisson-Charlier polynomials 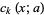 form a Sheffer sequence with
form a Sheffer sequence with
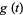 |
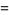 |
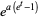 |
(1) |
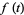 |
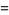 |
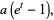 |
(2) |
giving the generating function
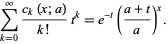 |
(3) |
The Sheffer identity is
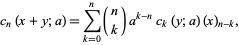 |
(4) |
where 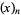 is a falling factorial (Roman 1984, p. 121). The polynomials satisfy the recurrence relation
is a falling factorial (Roman 1984, p. 121). The polynomials satisfy the recurrence relation
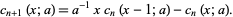 |
(5) |
These polynomials belong to the distribution 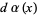 where
where 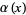 is a step function with jump
is a step function with jump
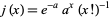 |
(6) |
at 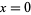 , 1, ... for
, 1, ... for 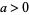 . They are given by the formulas
. They are given by the formulas
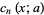 |
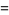 |
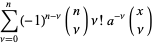 |
(7) |
 |
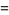 |
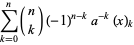 |
(8) |
 |
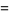 |
![a^n(-1)^n[j(x)]^(-1)Delta^nj(x-n)](http://mathworld.wolfram.com/images/equations/Poisson-CharlierPolynomial/Inline21.gif) |
(9) |
 |
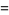 |
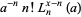 |
(10) |
 |
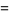 |
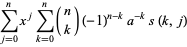 |
(11) |
where 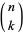 is a binomial coefficient,
is a binomial coefficient, 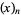 is a falling factorial,
is a falling factorial, 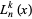 is an associated Laguerre polynomial,
is an associated Laguerre polynomial, 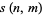 is a Stirling number of the first kind, and
is a Stirling number of the first kind, and
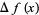 |
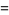 |
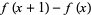 |
(12) |
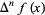 |
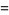 |
![Delta[Delta^(n-1)f(x)]=f(x+n)-(n; 1)f(x+n-1)+...+(-1)^nf(x).](http://mathworld.wolfram.com/images/equations/Poisson-CharlierPolynomial/Inline37.gif) |
(13) |
They are normalized so that
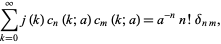 |
(14) |
where 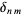 is the delta function.
is the delta function.
The first few polynomials are
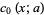 |
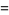 |
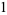 |
(15) |
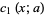 |
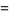 |
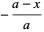 |
(16) |
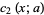 |
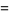 |
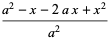 |
(17) |
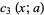 |
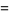 |
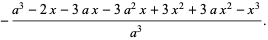 |
(18) |
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 2. New York: Krieger, p. 226, 1981.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, p. 473, 1965.
Roman, S. "The Poisson-Charlier Polynomials." §4.3.3 in The Umbral Calculus. New York: Academic Press, pp. 119-122, 1984.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 34-35, 1975.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|