


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-8-2019
Date: 3-6-2019
Date: 16-5-2018
|
A q-analog of Gauss's theorem due to Jacobi and Heine,
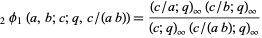 |
(1) |
for 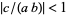 (Gordon and McIntosh 1997; Koepf 1998, p. 40), where
(Gordon and McIntosh 1997; Koepf 1998, p. 40), where 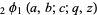 is a q-hypergeometric function. A special case for
is a q-hypergeometric function. A special case for 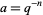 is given by
is given by
![sum_(k=0)^(n)q^(k^2)[n; k]_q^2](http://mathworld.wolfram.com/images/equations/q-GaussIdentity/Inline4.gif) |
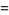 |
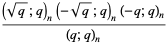 |
(2) |
 |
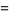 |
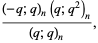 |
(3) |
where ![[n; k]_q](http://mathworld.wolfram.com/images/equations/q-GaussIdentity/Inline10.gif) is a q-binomial coefficient (Koepf 1998, p. 43).
is a q-binomial coefficient (Koepf 1998, p. 43).
REFERENCES:
Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 31, 1995.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 10 and 236, 1990.
Gordon, B. and McIntosh, R. J. "Algebraic Dilogarithm Identities." Ramanujan J. 1, 431-448, 1997.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|