


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-9-2019
Date: 2-5-2019
Date: 28-4-2019
|
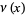 |
 |
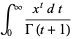 |
(1) |
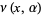 |
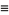 |
 |
(2) |
where 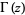 is the gamma function (Erdélyi et al. 1981, p. 217; Prudnikov et al. 1990, p. 799; Gradshteyn and Ryzhik 2000, p. 1109).
is the gamma function (Erdélyi et al. 1981, p. 217; Prudnikov et al. 1990, p. 799; Gradshteyn and Ryzhik 2000, p. 1109).
The notation 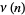 is also sometimes used to denote the divisor function
is also sometimes used to denote the divisor function 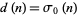 giving the number of divisors or the number of distinct prime factors
giving the number of divisors or the number of distinct prime factors 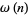 of a positive integer
of a positive integer 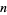 .
.
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Function 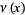 and Related Functions." §18.3 in Higher Transcendental Functions, Vol. 3. New York: Krieger, pp. 217-224, 1981.
and Related Functions." §18.3 in Higher Transcendental Functions, Vol. 3. New York: Krieger, pp. 217-224, 1981.
Gradshteyn, I. S. and Ryzhik, I. M. "The Functions 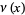 ,
, 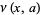 ,
, 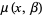 ,
, 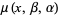 ,
, 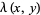 ." §9.64 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1109, 2000.
." §9.64 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1109, 2000.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, 1990.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|