المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Roman Factorial |
 1647
 11:55 صباحاً
date: 19-5-2019 |
Author : Loeb, D. E. 
Book or Source : "A Generalization of the Binomial Coefficients." 9 Feb 1995. http://arxiv.org/abs/math/9502218. 
Page and Part : ...|
Read More
Date: 28-7-2019
2565
Date: 12-10-2019
1719
Date: 26-9-2019
2096
|
![|_n]!={n! for n>=0; ((-1)^(-n-1))/((-n-1)!) for n<0.](http://mathworld.wolfram.com/images/equations/RomanFactorial/NumberedEquation1.gif) |
(1) |
The Roman factorial arises in the definition of the harmonic logarithm and Roman coefficient. It obeys the identities
![|_n]!=|_n]|_n-1]!](http://mathworld.wolfram.com/images/equations/RomanFactorial/NumberedEquation2.gif) |
(2) |
![(|_n]!)/(|_n-k]!)=|_n]|_n-1]...|_n-k+1]](http://mathworld.wolfram.com/images/equations/RomanFactorial/NumberedEquation3.gif) |
(3) |
![|_n]!|_-n-1]!=(-1)^(n+(n<0)),](http://mathworld.wolfram.com/images/equations/RomanFactorial/NumberedEquation4.gif) |
(4) |
where
![|_n]={n for n!=0; 1 for n=0](http://mathworld.wolfram.com/images/equations/RomanFactorial/NumberedEquation5.gif) |
(5) |
and
 |
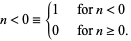(6) |
REFERENCES:
Loeb, D. E. "A Generalization of the Binomial Coefficients." 9 Feb 1995. http://arxiv.org/abs/math/9502218.
Loeb, D. and Rota, G.-C. "Formal Power Series of Logarithmic Type." Advances Math. 75, 1-118, 1989.
Roman, S. "The Logarithmic Binomial Formula." Amer. Math. Monthly 99, 641-648, 1992.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
