المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lemniscate Case |
 1720
 01:54 صباحاً
date: 23-4-2019 |
Author : Sloane, N. J. A 
Book or Source : Sequence A093341 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 19-9-2018
2004
Date: 4-8-2019
2046
Date: 23-8-2018
2801
|
The case of the Weierstrass elliptic function with invariants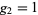 
and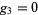 
. In this case, the half-periods are given by 
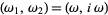, where 
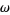is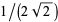 
times the lemniscate constant,
 |
 |
 |
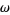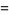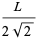(1) |
 |
 |
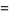![([Gamma(1/4)]^2)/(4sqrt(pi))](http://mathworld.wolfram.com/images/equations/LemniscateCase/Inline11.gif) |
(2) |
 |
 |
 |
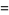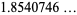(3) |
(OEIS A093341; Abramowitz and Stegun 1972, p. 658).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Lemniscate Case (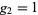
, 
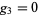)." §18.14 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 658-662, 1972.
Sloane, N. J. A. Sequence A093341 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
