


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2019
Date: 9-3-2017
Date: 19-1-2019
|
The Landau-Mignotte bound, also known as the Mignotte bound, is used in univariate polynomial factorization to determine the number of Hensel lifting steps needed. It gives an upper bound for the absolute value of coefficients of any nontrivial factor of a polynomial 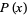 in
in ![Z[x]](http://mathworld.wolfram.com/images/equations/Landau-MignotteBound/Inline2.gif) .
.
The bound is given by
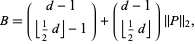 |
where 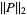 is the 2-norm and
is the 2-norm and
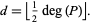 |
Factorization over the integers is done by factoring the polynomial modulo a "good" prime 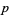 using the Berlekamp-Zassenhaus algorithm, and the irreducible factors are then lifted to ones modulo
using the Berlekamp-Zassenhaus algorithm, and the irreducible factors are then lifted to ones modulo 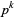 . There are guidelines for choosing
. There are guidelines for choosing 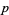 . For example,
. For example, 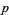 should not evenly divide the leading coefficient of the polynomial, and
should not evenly divide the leading coefficient of the polynomial, and 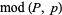 should be squarefree.
should be squarefree.
REFERENCES:
van Hoeij, M. "Factoring Polynomials and the Knapsack Problem." J. Number Th. 95, 167-189, 2002.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|