Algebraic Element

Given a field 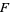 and an extension field 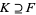, an element  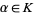is called algebraic over  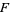if it is a root of some nonzero polynomial with coefficients in .

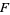Obviously, every element of 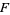 is algebraic over 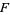. Moreover, the sum, difference, product, and quotient of algebraic elements are again algebraic. It follows that the simple extension field  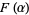is an algebraic extension o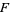f  iff 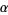 is algebraic over .

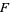The imaginary unit i is algebraic over the field 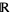 of real numbers since it is a root of the polynomial 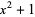. Because its coefficients are integers, it is even true that  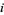is algebraic over the field  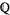of rational numbers, i.e., it is an algebraic number (and also an algebraic integer). As a consequence,  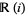and 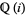 are algebraic extensions of  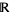and 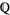respectively. (Here,  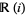is the complex field 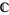, whereas  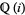is the total ring of fractions of the ring of Gaussian integers .)