


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-7-2018
Date: 13-7-2018
Date: 25-7-2018
|
A partial differential diffusion equation of the form
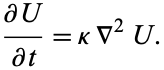 |
(1) |
Physically, the equation commonly arises in situations where 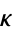 is the thermal diffusivity and
is the thermal diffusivity and 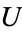 the temperature.
the temperature.
The one-dimensional heat conduction equation is
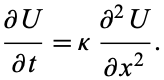 |
(2) |
This can be solved by separation of variables using
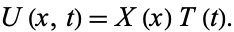 |
(3) |
Then
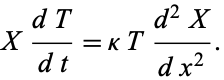 |
(4) |
Dividing both sides by 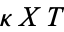 gives
gives
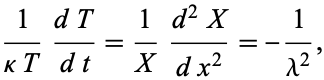 |
(5) |
where each side must be equal to a constant. Anticipating the exponential solution in 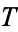 , we have picked a negative separation constant so that the solution remains finite at all times and
, we have picked a negative separation constant so that the solution remains finite at all times and 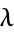 has units of length. The
has units of length. The 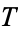 solution is
solution is
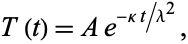 |
(6) |
and the 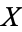 solution is
solution is
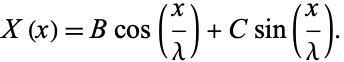 |
(7) |
The general solution is then
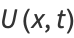 |
 |
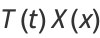 |
(8) |
 |
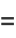 |
![Ae^(-kappat/lambda^2)[Bcos(x/lambda)+Csin(x/lambda)]](http://mathworld.wolfram.com/images/equations/HeatConductionEquation/Inline13.gif) |
(9) |
 |
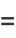 |
![e^(-kappat/lambda^2)[Dcos(x/lambda)+Esin(x/lambda)].](http://mathworld.wolfram.com/images/equations/HeatConductionEquation/Inline16.gif) |
(10) |
If we are given the boundary conditions
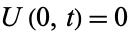 |
(11) |
and
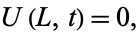 |
(12) |
then applying (11) to (10) gives
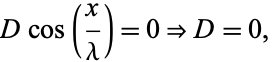 |
(13) |
and applying (12) to (10) gives
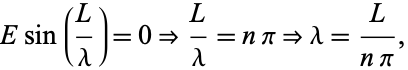 |
(14) |
so (10) becomes
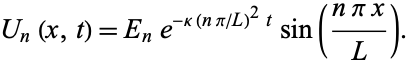 |
(15) |
Since the general solution can have any 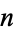 ,
,
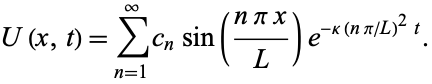 |
(16) |
Now, if we are given an initial condition 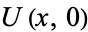 , we have
, we have
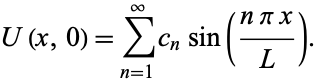 |
(17) |
Multiplying both sides by 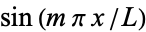 and integrating from 0 to
and integrating from 0 to 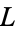 gives
gives
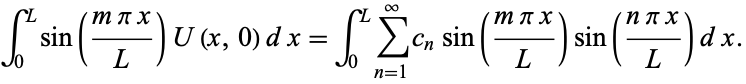 |
(18) |
Using the orthogonality of 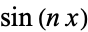 and
and 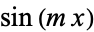 ,
,
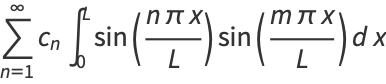 |
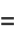 |
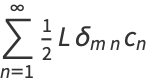 |
(19) |
 |
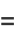 |
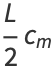 |
(20) |
 |
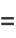 |
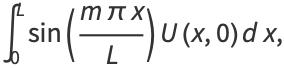 |
(21) |
so
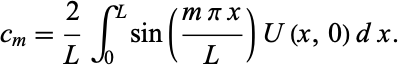 |
(22) |
If the boundary conditions are replaced by the requirement that the derivative of the temperature be zero at the edges, then (◇) and (◇) are replaced by
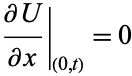 |
(23) |
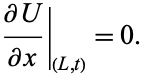 |
(24) |
Following the same procedure as before, a similar answer is found, but with sine replaced by cosine:
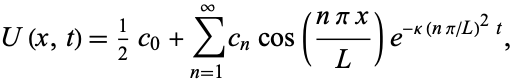 |
(25) |
where
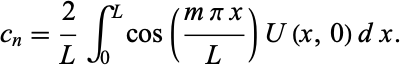 |
(26) |



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|