


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-5-2019
Date: 11-6-2019
Date: 29-8-2019
|
A real-valued univariate function 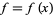 has a jump discontinuity at a point
has a jump discontinuity at a point 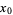 in its domain provided that
in its domain provided that
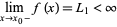 |
(1)
|
and
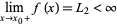 |
(2)
|
both exist and that 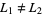 .
.
The notion of jump discontinuity shouldn't be confused with the rarely-utilized convention whereby the term jump is used to define any sort of functional discontinuity.
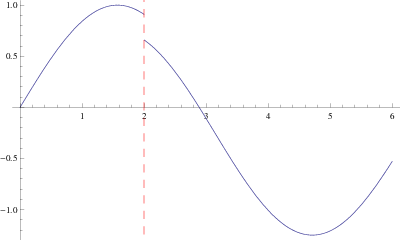
The figure above shows an example of a function having a jump discontinuity at a point in its domain.
Though less algebraically-trivial than removable discontinuities, jump discontinuities are far less ill-behaved than other types of singularities such as infinite discontinuities. This fact can be seen in a number of scenarios, e.g., in the fact that univariate monotone functions can have at most countably many discontinuities (Royden and Fitzpatrick 2010), the worst of which can be jump discontinuities (Zakon 2004).
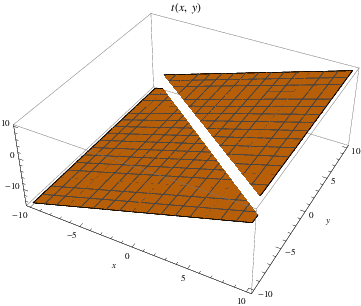
Unsurprisingly, the definition given above can be generalized to include jump discontinuities in multivariate real-valued functions as well. For example, the function shown in this figure is the piecewise function
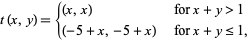 |
(3)
|
a function which is monotone in each of  and
and 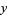 separately and has jump discontinuity along the entire line
separately and has jump discontinuity along the entire line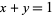
REFERENCES:
Royden, H. L. and Fitzpatrick, P. M. Real Analysis. Pearson, 2010.
Zakon, E. Mathematical Analysis Volume 1. West Lafayette, IN: The Trilla Group, 2004. http://www.trillia.com/zakon-analysisI.html.
.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: الامين العام للعتبة الحسينية يكرم المساهمين في انجاح الختمة القرآنية المركزية في الصحن الحسيني
|
|
|