
Compound Interest
 المؤلف:
W.D. Wallis
المؤلف:
W.D. Wallis
 المصدر:
Mathematics in the Real World
المصدر:
Mathematics in the Real World
 الجزء والصفحة:
208-209
الجزء والصفحة:
208-209
 15-2-2016
15-2-2016
 1966
1966
When dealing with compound interest, students will find it very useful if their calculator enables them to calculate powers of numbers: for example, if it has a key (possibly one marked xy) that enables the user to input two numbers and automatically calculate the result of raising the first number to the power of the second number. (Only positive whole number powers will occur).
Say you have $100 and every year you double your money.
One year from now you have $200.
2 years from now you have $400.
3 years from now you have $800.
So in 1 year you gain 100%; in 3 years you gain 700%—much more than
3×100%. This process is called compounding. It also happens for interest less than 100%.
Sample Problem 1.1 Suppose you put $1,000 in the bank for 5 years at 10% interest paid annually. If you take your interest out of the bank at the end of each year, how much do you have at the end of 5 years? If you allow it to compound, how much do you have at the end of 5 years?
Solution. If you take your interest out of the bank at the end of each year, you get $100 each year. After 5 years you have a total of $1500, a profit of $500.
If you put your interest back in the bank at 10%:
• After year 1 you get $100, so you have a total of $1100 in the bank.
• After year 2 you get $110 (10% of $1100), so you have a total of $1210 in the bank.
• After year 3 you get $121, for a total of $1331.
• After year 4 get $133.10, for a total of $1464.10.
• After year 5 get $146.41, for a total of $1610.51.
So after 5 years you have $1610.51, a profit of $610.
Let’s look at this in general. Say you put $P in the bank at R% for N years, and reinvest all the interest. You end up with
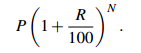
This process is called geometric growth.
On the other hand, simple interest is the same as “we’ll take the interest out each year.” After N years at R% you would finish with
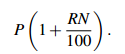
This is called arithmetic growth.
Sample Problem 1.2 Suppose you invest $1,200 at 10% interest for 3 years with interest paid each year. How much interest is earned in total, if you take the interest out each year? How much if you reinvest the interest each year?
Solution. We use the two formulas. For arithmetic growth, you end with
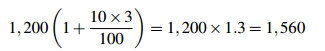
and the interest is $(1,560 − 1,200) = $360. Under geometric growth, the amount received after 3 years is
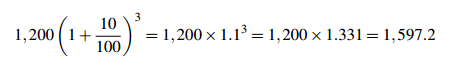
and the interest is $397.20.
 الاكثر قراءة في الرياضيات في العلوم الاخرى
الاكثر قراءة في الرياضيات في العلوم الاخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


