σ orbitals
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص372-373
2025-11-27
67
σ orbitals
Consider H2, the simplest many-electron diatomic molecule. Each H atom con tributes a 1s orbital (as in H2+), so we can form the 1σg and 1σu orbitals from them, as we have seen already. At the experimental internuclear separation these orbitals will have the energies shown in Fig. 11.23, which is called a molecular orbital energy level diagram. Note that from two atomic orbitals we can build two molecular orbitals. In general, from N atomic orbitals we can build N molecular orbitals. There are two electrons to accommodate, and both can enter 1σg by pairing their spins, as required by the Pauli principle (see the following Justification). The ground state configuration is therefore 1σg 2 and the atoms are joined by a bond consisting of an electron pair in a bonding σ orbital. This approach shows that an electron pair, which was the focus of Lewis’s account of chemical bonding, represents the maximum number of electrons that can enter a bonding molecular orbital.
Justification 11.2 Electron pairing in MO theory The spatial wavefunction for two electrons in a bonding molecular orbital ψ such as the bonding orbital in eqn 11.7, is ψ(1)ψ(2). This two-electron wavefunction is obviously symmetric under interchange of the electron labels. To satisfy the Pauli principle, it must be multiplied by the antisymmetric spin state α(1)β(2) − β(1)α(2) to give the overall antisymmetric state
ψ (1,2) = ψ(1)ψ(2){α(1)β(2) − β(1)α(2)}
Because α (1)β(2) − β(1)α(2) corresponds to paired electron spins, we see that two electrons can occupy the same molecular orbital (in this case, the bonding orbital) only if their spins are paired.
The same argument shows why He does not form diatomic molecules. Each He atom contributes a 1s orbital, so 1σg and 1σu molecular orbitals can be constructed. Although these orbitals differ in detail from those in H2, the general shape is the same, and we can use the same qualitative energy level diagram in the discussion. There are four electrons to accommodate. Two can enter the 1σg orbital, but then it is full, and the next two must enter the 1σu orbital (Fig. 11.24). The ground electronic configuration of He2 is therefore 1σg 21σu 2. We see that there is one bond and one anti-bond. Because an anti -bond is slightly more antibonding than a bond is bonding, an He2 molecule has a higher energy than the separated atoms, so it is unstable relative to the individual atoms. We shall now see how the concepts we have introduced apply to homonuclear diatomic molecules in general. In elementary treatments, only the orbitals of the valence shell are used to form molecular orbitals so, for molecules formed with atoms from Period 2 elements, only the 2s and 2p atomic orbitals are considered. A general principle of molecular orbital theory is that all orbitals of the appropriate symmetry contribute to a molecular orbital. Thus, to build σ orbitals, we form linear combinations of all atomic orbitals that have cylindrical symmetry about the inter nuclear axis. These orbitals include the 2s orbitals on each atom and the 2pz orbitals on the two atoms (Fig. 11.25). The general form of the σ orbitals that may be formed is therefore
ψ=cA2s χA2s + cB2s χB2s + cA2pz χA2pz + cB2pz χB2pz
From these four atomic orbitals we can form four molecular orbitals of σ symmetry by an appropriate choice of the coefficients c. The procedure for calculating the coefficients will be described in Section 11.6. At this stage we adopt a simpler route, and suppose that, because the 2s and 2pz orbitals have distinctly different energies, they may be treated separately. That is, the four σ orbitals fall approximately into two sets, one consisting of two molecular orbitals of the form
ψ=cA2s χA2s + cB2s χB2s
and another consisting of two orbitals of the form ψ=cA2pz χA2pz + cB2pz χB2pz
Because atoms A and B are identical, the energies of their 2s orbitals are the same, so the coefficients are equal (apart from a possible difference in sign); the same is true of the 2pz orbitals. Therefore, the two sets of orbitals have the form χA2s ± χB2s and χA2pz ± χB2pz. The 2s orbitals on the two atoms overlap to give a bonding and an antibonding σ orbital (1σg and 1σu, respectively) in exactly the same way as we have already seen for 1s orbitals. The two 2pz orbitals directed along the internuclear axis overlap strongly. They may interfere either constructively or destructively, and give a bonding or anti bonding σ orbital, respectively (Fig. 11.26). These two σ orbitals are labelled 2σg and 2σu, respectively. In general, note how the numbering follows the order of increasing energy.
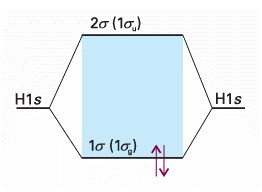
Fig. 11.23 A molecular orbital energy level diagram for orbitals constructed from the overlap of H1s orbitals; the separation of the levels corresponds to that found at the equilibrium bond length. The ground electronic configuration of H2 is obtained by accommodating the two electrons in the lowest available orbital (the bonding orbital).
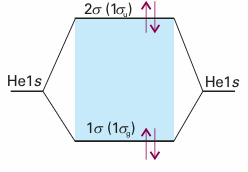
Fig. 11.24 The ground electronic configuration of the hypothetical four electron molecule He2 has two bonding electrons and two antibonding electrons. It has a higher energy than the separated atoms, and so is unstable.
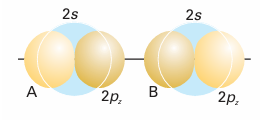
Fig. 11.25 According to molecular orbital theory, σ orbitals are built from all orbitals that have the appropriate symmetry. In homonuclear diatomic molecules of Period 2, that means that two 2s and two 2pz orbitals should be used. From these four orbitals, four molecular orbitals can be built.
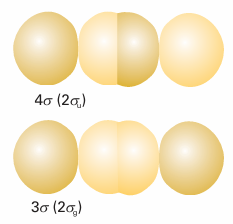
Fig. 11.26 A representation of the composition of bonding and antibonding σ orbitals built from the overlap of p orbitals. These illustrations are schematic.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
