The variation of the Gibbs energy with pressure
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص108-109
2025-11-09
46
The variation of the Gibbs energy with pressure
To find the Gibbs energy at one pressure in terms of its value at another pressure, the temperature being constant, we set dT = 0 in eqn 3.49, which gives dG = Vdp, and integrate:
For molar quantities,
This expression is applicable to any phase of matter, but to evaluate it we need to know how the molar volume, Vm, depends on the pressure. The molar volume of a condensed phase changes only slightly as the pressure changes (Fig. 3.21), so we can treat Vm as a constant and take it outside the integral:
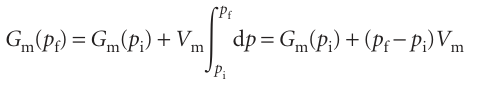
Under normal laboratory conditions (pf −pi) Vm is very small and may be neglected. Hence, we may usually suppose that the Gibbs energies of solids and liquids are independent of pressure. However, if we are interested in geophysical problems, then because pressures in the Earth’s interior are huge, their effect on the Gibbs energy cannot be ignored. If the pressures are so great that there are substantial volume changes over the range of integration, then we must use the complete expression, eqn 3.54.
Illustration 3.10
Suppose that for a certain phase transition of a solid ∆trsV =+1.0 cm3 mol−1 independent of pressure. Then, for an increase in pressure to 3.0 Mbar (3.0 × 1011 Pa) from 1.0 bar (1.0 × 105 Pa), the Gibbs energy of the transition changes from ∆trsG (1 bar) to ∆trsG (3 Mbar) =∆trsG (1 bar) +(1.0×10−6m3mol−1) ×(3.0×1011Pa−1.0×105Pa) =∆trsG (1 bar) + 3.0 × 102 kJ mol−1
where we have used 1 Pa m3 = 1 J.
Fig. 3.21 The difference in Gibbs energy of a solid or liquid at two pressures is equal to the rectangular area shown. We have assumed that the variation of volume with pressure is negligible.
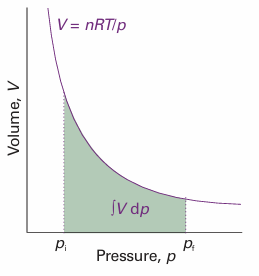
Fig. 3.22 The difference in Gibbs energy for a perfect gas at two pressures is equal to the area shown below the perfect-gas isotherm.
The molar volumes of gases are large, so the Gibbs energy of a gas depends strongly on the pressure. Furthermore, because the volume also varies markedly with the pressure, we cannot treat it as a constant in the integral in eqn 3.54b (Fig. 3.22).
For a perfect gas we substitute Vm=RT/p into the integral, treat RT as a constant, and find
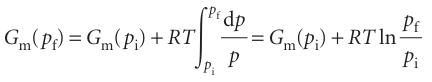
This expression shows that when the pressure is increased tenfold at room temperature, the molar Gibbs energy increases by RT ln 10 ≈ 6 kJ mol−1. It also follows from this equation that, if we set pi=p7(the standard pressure of 1 bar), then the molar Gibbs energy of a perfect gas at a pressure p (set pf=p) is related to its standard value by
The logarithmic dependence of the molar Gibbs energy on the pressure predicted by eqn 3.57 is illustrated in Fig. 3.23. This very important expression, the consequences of which we unfold in the following chapters, applies to perfect gases (which is usually a good enough approximation). Further information 3.2describes how to take into account gas imperfections.
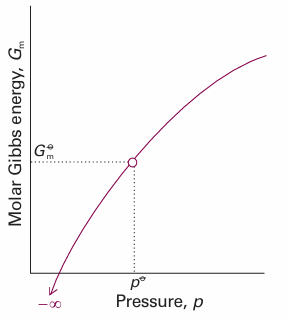
Fig. 3.23The molar Gibbs energy potential of a perfect gas is proportional to ln p, and the standard state is reached at p7. Note that, as p→0, the molar Gibbs energy becomes negatively infinite.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
