General considerations
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص 105-107
2025-11-09
47
General considerations
When the system undergoes a change of state, G may change because H, T, and S all change. As in Justification 2.1, we write for infinitesimal changes in each property , dG=dH−d(TS)=dH−TdS−SdT , Because H =U+pV, we know that , dH=dU+d(pV)=dU+pdV+Vdp , and therefore , dG=dU+pdV+Vdp−TdS−SdT , For a closed system doing no non-expansion work, we can replace dU by the funda mental equation dU = TdS − pdV and obtain , dG=TdS−pdV+pdV+Vdp−TdS−SdT , Four terms now cancel on the right, and we conclude that, for a closed system in the absence of non-expansion work and at constant composition, dG=Vdp−SdT , This expression, which shows that a change in G is proportional to a change in p or T, suggests that G may be best regarded as a function of p and T. It confirms that G is an important quantity in chemistry because the pressure and temperature are usually the variables under our control. In other words, G carries around the combined consequences of the First and Second Laws in a way that makes it particularly suitable for chemical applications. , The same argument that led to eqn 3.45, when applied to the exact differential dG =Vdp−SdT, now gives
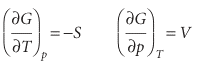
These relations show how the Gibbs energy varies with temperature and pressure (Fig. 3.18). The first implies that: • Because S>0 for all substances, G always decreases when the temperature is raised (at constant pressure and composition). • Because (∂G/∂T)p becomes more negative as S increases, G decreases most sharply when the entropy of the system is large. Therefore, the Gibbs energy of the gaseous phase of a substance, which has a high molar entropy, is more sensitive to temperature than its liquid and solid phases (Fig. 3.19). Similarly, the second relation implies that: • Because V > 0 for all substances, G always increases when the pressure of the system is increased (at constant temperature and composition).
Fig. 3.18 The variation of the Gibbs energy of a system with (a) temperature at constant pressure and (b) pressure at constant temperature. The slope of the former is equal to the negative of the entropy of the system and that of the latter is equal to the volume.
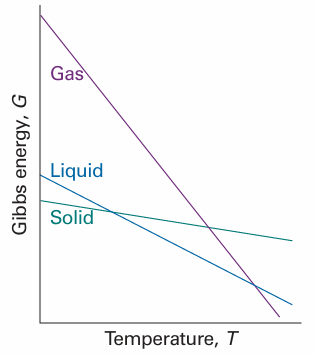
Fig. 3.19 The variation of the Gibbs energy with the temperature is determined by the entropy. Because the entropy of the gaseous phase of a substance is greater than that of the liquid phase, and the entropy of the solid phase is smallest, the Gibbs energy changes most steeply for the gas phase, followed by the liquid phase, and then the solid phase of the substance.
Because (∂G/∂p)T increases with V,Gis more sensitive to pressure when the volume of the system is large. Because the molar volume of the gaseous phase of a substance is greater than that of its condensed phases, the molar Gibbs energy of a gas is more sensitive to pressure than its liquid and solid phases (Fig. 3.20).
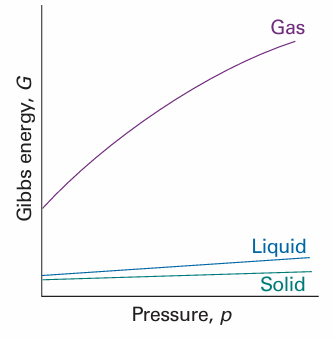
Fig. 3.20The variation of the Gibbs energy with the pressure is determined by the volume of the sample. Because the volume of the gaseous phase of a substance is greater than that of the same amount of liquid phase, and the entropy of the solid phase is smallest (for most substances), the Gibbs energy changes most steeply for the gas phase, followed by the liquid phase, and then the solid phase of the substance. Because the volumes of the solid and liquid phases of a substance are similar, their molar Gibbs energies vary by similar amounts as the pressure is changed.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
