Convex Function
المؤلف:
Eggleton, R. B. and Guy, R. K.
المصدر:
"Catalan Strikes Again! How Likely is a Function to be Convex?" Math. Mag. 61
الجزء والصفحة:
...
18-7-2021
1851
Convex Function
A convex function is a continuous function whose value at the midpoint of every interval in its domain does not exceed the arithmetic mean of its values at the ends of the interval.
More generally, a function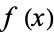 
is convex on an interval ![[a,b]](https://mathworld.wolfram.com/images/equations/ConvexFunction/Inline2.gif)
if for any two points 
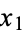and 
in ![[a,b]](https://mathworld.wolfram.com/images/equations/ConvexFunction/Inline5.gif)
and any 
where 
,
(Rudin 1976, p. 101; cf. Gradshteyn and Ryzhik 2000, p. 1132).
If 
has a second derivative in ![[a,b]](https://mathworld.wolfram.com/images/equations/ConvexFunction/Inline9.gif)
, then a necessary and sufficient condition for it to be convex on that interval is that the second derivative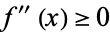 
for all 
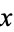in ![[a,b]](https://mathworld.wolfram.com/images/equations/ConvexFunction/Inline12.gif)
.
If the inequality above is strict for all 
and 
, then 
is called strictly convex.
Examples of convex functions include 
for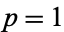 
or even 
, 
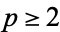for 
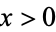, and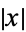 
for all 
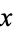. If the sign of the inequality is reversed, the function is called concave.
REFERENCES:
Eggleton, R. B. and Guy, R. K. "Catalan Strikes Again! How Likely is a Function to be Convex?" Math. Mag. 61, 211-219, 1988.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1132, 2000.
Rudin, W. Principles of Mathematical Analysis, 3rd ed. New York: McGraw-Hill, 1976.
Webster, R. Convexity. Oxford, England: Oxford University Press, 1995.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
