Maximum Likelihood
المؤلف:
Harris, J. W. and Stocker, H.
المصدر:
"Maximum Likelihood Method." §21.10.4 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag,
الجزء والصفحة:
...
15-2-2021
1764
Maximum Likelihood
Maximum likelihood, also called the maximum likelihood method, is the procedure of finding the value of one or more parameters for a given statistic which makes the known likelihood distribution a maximum. The maximum likelihood estimate for a parameter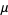 
is denoted 
.
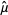For a Bernoulli distribution,
![d/(dtheta)[(N; Np)theta^(Np)(1-theta)^(Nq)]=Np(1-theta)-thetaNq=0,](https://mathworld.wolfram.com/images/equations/MaximumLikelihood/NumberedEquation1.gif) |
(1)
|
so maximum likelihood occurs for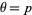 
. If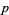 
is not known ahead of time, the likelihood function is
where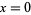 
or 1, and 
, ..., 
.
 |
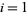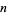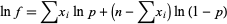(5)
|
 |
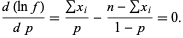(6)
|
Rearranging gives
 |
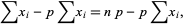(7)
|
so
 |
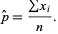(8)
|
For a normal distribution,
so
 |
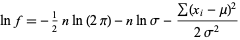(11)
|
and
 |
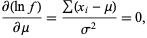(12)
|
giving
 |
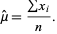(13)
|
Similarly,
 |
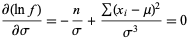(14)
|
gives
 |
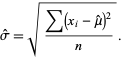(15)
|
Note that in this case, the maximum likelihood standard deviation is the sample standard deviation, which is a biased estimator for the population standard deviation.
For a weighted normal distribution,
 |
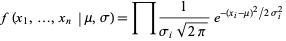(16)
|
 |
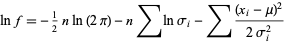(17)
|
 |
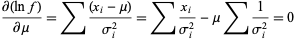(18)
|
gives
 |
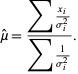(19)
|
The variance of the mean is then
 |
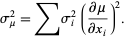(20)
|
But
 |
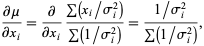(21)
|
so
For a Poisson distribution,
 |
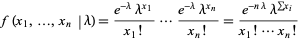(25)
|
 |
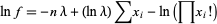(26)
|
 |
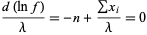(27)
|
 |
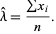(28)
|
REFERENCES:
Harris, J. W. and Stocker, H. "Maximum Likelihood Method." §21.10.4 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 824, 1998.
Hoel, P. G. Introduction to Mathematical Statistics, 3rd ed. New York: Wiley, p. 57, 1962.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Least Squares as a Maximum Likelihood Estimator." §15.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 651-655, 1992.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
