Euler,s Number Triangle
المؤلف:
Sloane, N. J. A.
المصدر:
Sequence A008292 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
7-1-2021
1784
Euler's Number Triangle
The triangle of numbers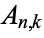 
given by
 |
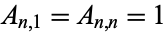(1)
|
and the recurrence relation
 |
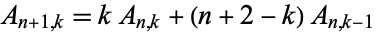(2)
|
for ![k in [2,n]](https://mathworld.wolfram.com/images/equations/EulersNumberTriangle/Inline2.gif)
, where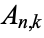 
are shifted Eulerian numbers, i.e.,
 |
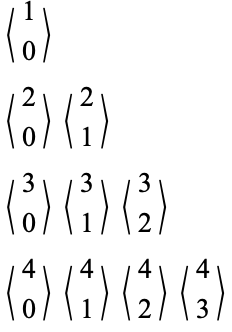(3)
|
 |
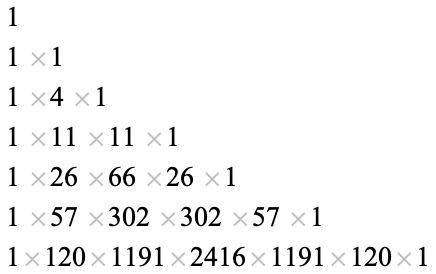(4)
|
(OEIS A008292). Note that the rows sum to the successive factorials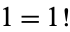 
, 
, 
, 
, ....
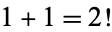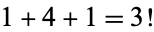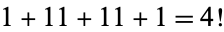The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Euler's number triangle.
Amazingly, the Z-transform of ![<span style=]()
{n^k}_(k=1)^N" src="https://mathworld.wolfram.com/images/equations/EulersNumberTriangle/Inline8.gif" style="height:22px; width:42px" /> is the generator for the first 
rows of Euler's number triangle, when the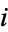 
th term of the transform is first cleared of its denominator by multiplying through by 
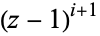. For example,
![Z[<span style=]() {n^k}_(k=1)^3={z/((z-1)^2),(z+z^2)/((z-1)^3),(z+4z^2+z^3)/((z-1)^4)}. " src="https://mathworld.wolfram.com/images/equations/EulersNumberTriangle/NumberedEquation5.gif" style="height:43px; width:282px" /> |
(5)
|
REFERENCES:
Sloane, N. J. A. Sequence A008292 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
