Binomial Number
المؤلف:
Sloane, N. J. A
المصدر:
Sequences A000005/M0246 and A001227 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
30-12-2020
1162
Binomial Number
A binomial number is a number of the form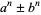 
, where 
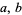, and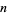 
are integers. Binomial numbers can be factored algebraically as
 |
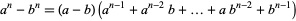(1)
|
for all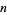 
,
 |
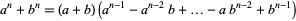(2)
|
for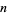 
odd, and
![a^(nm)-b^(nm)=(a^m-b^m)[a^(m(n-1))+a^(m(n-2))b^m+...+b^(m(n-1))].](https://mathworld.wolfram.com/images/equations/BinomialNumber/NumberedEquation3.gif) |
(3)
|
for all positive integers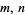 
. For example,
and
Rather surprisingly, the number of factors of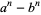 
with 
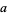and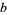 
symbolic and 
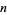a positive integer is given by 
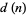, where 
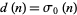is the number of divisors of 
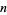and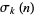 
is the divisor function. The first few terms are therefore 1, 2, 2, 3, 2, 4, 2, ... (OEIS A000005).
Similarly, the number of factors of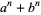 
is given by 
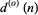, where 
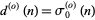is the number of odd divisors of 
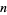and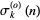 
is the odd divisor function. The first few terms are therefore 1, 1, 2, 1, 2, 2, 2, 1,... (OEIS A001227).
In 1770, Euler proved that if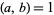 
, then every odd factor of
 |
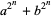(22)
|
is of the form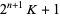 
. (A number of the form 
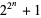is called a Fermat number.)
If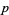 
and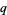 
are primes, then
 |
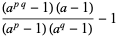(23)
|
is divisible by every prime factor of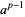 
not dividing 
.
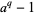REFERENCES:
Guy, R. K. "When Does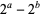 
Divide 
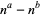." §B47 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 102, 1994.
Qi, S and Ming-Zhi, Z. "Pairs where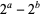 
Divides 
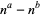for All 
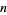." Proc. Amer. Math. Soc. 93, 218-220, 1985.
Schinzel, A. "On Primitive Prime Factors of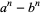 
." Proc. Cambridge Phil. Soc. 58, 555-562, 1962.
Sloane, N. J. A. Sequences A000005/M0246 and A001227 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
