A number is said to be squarefree (or sometimes quadratfrei; Shanks 1993) if its prime decomposition contains no repeated factors. All primes are therefore trivially squarefree. The number 1 is by convention taken to be squarefree. The squarefree numbers are 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, ... (OEIS A005117). The squareful numbers (i.e., those that contain at least one square) are 4, 8, 9, 12, 16, 18, 20, 24, 25, ... (OEIS A013929).

The Wolfram Language function SquareFreeQ[n] determines whether a number is squarefree. Note that for technical reasons, the Wolfram Language considers 1 to be squarefree, a convention that is consistent with defining a number to be squarefree when 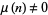, where  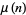is the Möbius function. The number 1 therefore has the somewhat curious distinction of being simultaneously a perfect square and squarefree.

Let 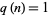 where 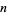 is squarefree and  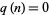where 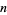 contains one or more squares, so that 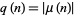. Then

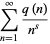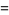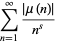			(1)
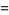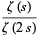			(2)

for 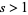 and 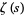 is the Riemann zeta function (Hardy and Wright 1979, p. 255).

The values of the first 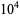 integers are plotted above on a  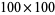grid, with squarefree values shown in white. Clear patterns emerge where multiples of numbers each share one or more repeated factor.

There is no known polynomial time algorithm for recognizing squarefree integers or for computing the squarefree part of an integer. In fact, this problem may be no easier than the general problem of integer factorization (obviously, if an integer 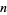 can be factored completely,  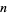is squarefree iff it contains no duplicated factors). This problem is an important unsolved problem in number theory because computing the ring of integers of an algebraic number field is reducible to computing the squarefree part of an integer (Lenstra 1992, Pohst and Zassenhaus 1997).

All numbers less than 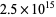 in Sylvester's sequence are squarefree, and no squareful numbers in this sequence are known (Vardi 1991). Every Carmichael number is squarefree. The binomial coefficients  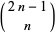are squarefree only for 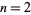, 3, 4, 6, 9, 10, 12, 36, ..., with no others less than 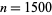. The central binomial coefficients are squarefree only for 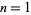, 2, 3, 4, 5, 7, 8, 11, 17, 19, 23, 71, ... (OEIS A046098), with no others less than 1500.

Let 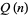 be the number of positive squarefree numbers  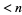(Hardy and Wright 1979, p. 251). Then for 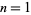, 2, ..., the first few values are 0, 1, 2, 3, 3, 4, 5, 6, 6, 6, 7, 8, 8, 9, 10, 11, 11, ... (OEIS A013928). Sums for  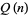include

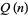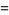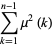			(3)
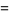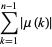			(4)
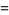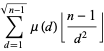			(5)
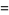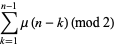			(6)
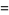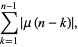			(7)

where 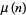 is the Möbius function.

The asymptotic number 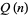 of squarefree numbers  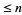is given by

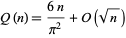(8)

(Landau 1974, pp. 604-609; Nagell 1951, p. 130; Hardy and Wright 1979, pp. 269-270; Hardy 1999, p. 65). The asymptotic density is therefore 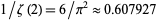 (OEIS A059956; Wells 1986, p. 28; Borwein and Bailey 2003, p. 139), where  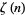is the Riemann zeta function. The values of  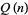for 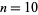, 100, 1000, ... are 7, 61, 608, 6083, 60794, 607926, 6079291, 60792694, 607927124, 6079270942, ... (OEIS A071172).

Similarly, the asymptotic density of squarefree Gaussian integers is given by 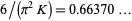 (OEIS A088454), where  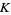is Catalan's constant (Pegg; Collins and Johnson 1989; Finch 2003, p. 601).

The Möbius function is given by

{0 if n has one or more repeated prime factors; 1 if n=1; (-1)^k if n is product of k distinct primes, " src="https://mathworld.wolfram.com/images/equations/Squarefree/NumberedEquation2.gif" style="height:64px; width:341px" />

(9)

so 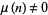 indicates that  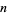is squarefree. The asymptotic formula for  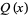is equivalent to the formula

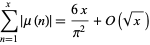(10)

(Hardy and Wright 1979, p. 270)

Let 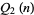 be the number of consecutive numbers  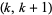with 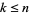 such that  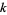and 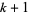 are both squarefree.  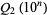for 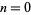, 1, ... are given by 1, 5, 33, 323, 3230, 32269, 322619, 3226343, 32263377, 322634281, 3226340896, ... (OEIS A087618). Then  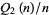is given asymptotically by

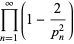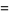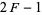			(11)
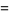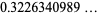			(12)

(OEIS A065474; Carlitz 1932, Heath-Brown 1984), where 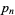 is the 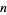th prime and  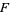is the Feller-Tornier constant.

REFERENCES:

Bellman, R. and Shapiro, H. N. "The Distribution of Squarefree Integers in Small Intervals." Duke Math. J. 21, 629-637, 1954.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Carlitz, L. "On a Problem in Additive Arithmetic. II." Quart. J. Math. 3, 273-290, 1932.

Collins, G. E. and Johnson, J. R. "The Probability of Relative Primality of Gaussian Integers." Proc. 1988 Internat. Sympos. Symbolic and Algebraic Computation (ISAAC), Rome (Ed. P. Gianni). New York: Springer-Verlag, pp. 252-258, 1989.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hardy, G. H. and Wright, E. M. "The Number of Squarefree Numbers." §18.6 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 269-270, 1979.

Heath-Brown, D. R. "The Square Sieve and Consecutive Square-Free Numbers." Math. Ann. 266, 251-259, 1984.

Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, 1974.

Lenstra, H. W. Jr. "Algorithms in Algebraic Number Theory." Bull. Amer. Math. Soc. 26, 211-244, 1992.

Nagell, T. Introduction to Number Theory. New York: Wiley, p. 130, 1951.

Pegg, E. Jr. "The Neglected Gaussian Integers." https://www.mathpuzzle.com/Gaussians.html.

Pohst, M. and Zassenhaus, H. Algorithmic Algebraic Number Theory. Cambridge, England: Cambridge University Press, p. 429, 1997.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 114, 1993.

Sloane, N. J. A. Sequences A005117/M0617, A013928, A013929, A046098, A059956, A065474, A071172, A087618, and A088454 in "The On-Line Encyclopedia of Integer Sequences."

Vardi, I. "Are All Euclid Numbers Squarefree?" §5.1 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 7-8, 82-85, and 223-224, 1991.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

وفد العتبة العباسية المقدسة يهنئ الأمين العام للعتبة الكاظمية المقدسة بمناسبة تعيينه

العتبة العباسية المقدسة تنظم دورة في الإسعافات الأولية لعدد من ملاكاتها

في مستشفى الكفيل.. فريق طبي ينجح بمعالجة مسن يعاني من انسداد القناة الصفراوية

المجمع العلمي يقيم جلسةً قرآنية لتعليم أحكام التلاوة في النجف الأشرف

المزيد

الآخبار الصحية

الأطعمة الحارة.. "سر صغير" يغير صحة قلبك وعقلك

وباء صامت.. الملايين حول العالم مصابون بالسكري دون أن يعلموا !

لماذا ينصح بتناول تفاحة يوميا؟

8 فواكه طبيعية تمنحك نوما هنيئا.. وتخلصك من الأرق

المزيد

الآخبار التكنلوجية

ثلاث علامات على وجود مشاكل خطيرة في محرك السيارة ؟

ماذا نعرف عن اللقاح الروسي ضد السرطان؟

مركبة فضاء تعثر على دليل عن وجود حياة قديمة على المريخ

لتدريب الذكاء الاصطناعي.. الصين تخطط لإنشاء شبكة حوسبة موحدة

المزيد