Hexagonal Square Number
المؤلف:
Sloane, N. J. A.
المصدر:
Sequences A008844, A046176, and A046177 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
18-12-2020
1219
Hexagonal Square Number
Let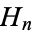 
denote the 
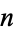th hexagonal number and 
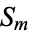the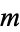 
th square number, then a number which is both hexagonal and square satisfies the equation 
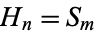, or
 |
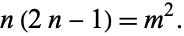(1)
|
Completing the square and rearranging gives
 |
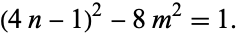(2)
|
Therefore, defining
gives the Pell equation
 |
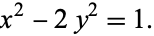(5)
|
The first few solutions are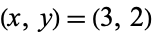 
, (17, 12), (99, 70), (577, 408), .... These give the solutions 
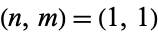, (9/2, 6), (25, 35), (289/2, 204), ..., giving the integer solutions (1, 1), (25, 35), (841, 1189), (28561, 40391), ... (OEIS A008844 and A046176). The corresponding hexagonal square numbers are 1, 1225, 1413721, 1631432881, 1882672131025, ... (OEIS A046177).
Closed-form solutions are
giving the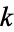 
th hexagonal square number as
![HS_k=1/(32)[-2+(17-12sqrt(2))(3-2sqrt(2))^(4k)+(17+12sqrt(2))(3+2sqrt(2))^(4k)].](https://mathworld.wolfram.com/images/equations/HexagonalSquareNumber/NumberedEquation4.gif) |
(8)
|
A recurrence relation for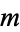 
is given by
 |
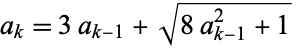(9)
|
with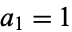 
, where 
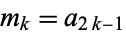(M. Carreira, pers. comm., Sept. 11, 2004).
REFERENCES:
Sloane, N. J. A. Sequences A008844, A046176, and A046177 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
