حل معادلة شرودنجر
المؤلف:
الدكتور صلاح الدين محمود يونس
المصدر:
الفيزياء الجزيئية
الجزء والصفحة:
87
18-11-2020
5494
حل معادلة شرودنجر
بإهمال الحركة الانتقالية للجزيئة نبحث المعادلة الآتية:
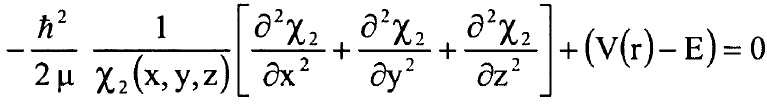..................(1)
حيث E تمثل طاقة الجزيئة الداخلية الدورانية والاهتزازية وفي ما يلي سنستبدل الدالة χ2 بالدالة χ ومعلوم ان المقصود هو χ2 ويمكن كتابة معادلة شرودنجر (1) بالصيغة:
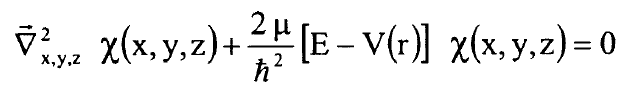......................(2)
ويمكن حل المعادلة (2) بالاحداثيات الكروية القطبية بفصل المتغيرات وكتابة الحل كحاصل ضرب ثلاث دوال:
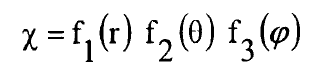..............(3)
بتعويض المعادلة (3) في المعادلة (2) نصل الى:
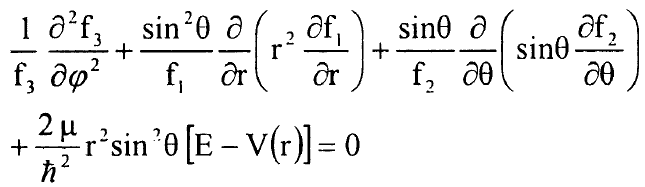....................(4)
حيث اصبحت المعادلة جمع حدود مستقلة وكل حد يحتوي متغير واحد فقط ولكي تكون ممكنة يجب ان يساوي كل حد مقدارا ثابتا ولذلك ناخذ الحد الاول مساويا الى الثالث α والحد الاخير مساويا الى α – ويجب ان تصح هذه العلاقة: α = - m2 حيث m عدد حقيقي وعندئذ يكون الحل للجزء الثالث بالشكل:
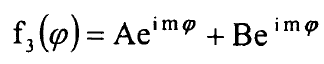
ولان الدالة الموجية يجب ان تكون احادية القيمة فيجب ان يكون لها نفس القيمة بعد اضافة π2 لذلك يجب ان ياخذ العدد m القيم الصحيحة التالية:
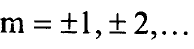
وبعد قسمة المعادلة (4) على sin2θ نحصل على التعبير:
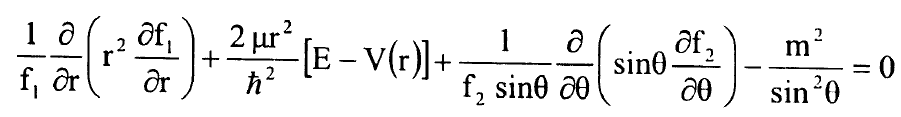..................(5)
ولكي تتحقق المعادلة (5) يجب ان تصح العلاقة:
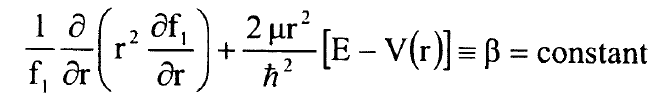...............(6)
وايضا تصح العلاقة:
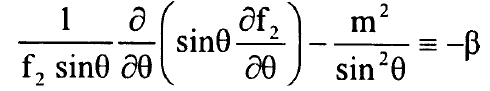................(7)
ان المعادلة (6) تحتوي المتغير r فقط والمعادلة (7) تضم المتغير r فقط ويمكن حل المعادلة (7) بواسطة المتوالية:
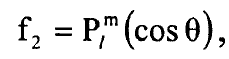
حيث / دليل المتوالية و (β= l (l +1 وm دليل وليس اس. ان الدوال Pl تدعى متعددة حدود ليجندر واذا وضعنا cos θ = u نصل الى:
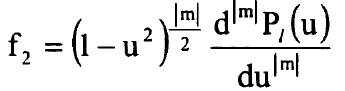
حيث:
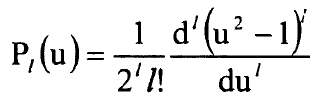
ويتحقق الشرط:
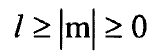
حيث / العدد الكمي للزخم الزاوي وتصبح الان المعادلة (6) بالشكل:
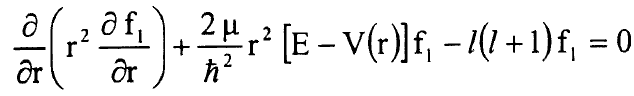....................(8)
ان المعادلة (8) هي المعادلة النصف قطرية والتي يمكن ايجاد حلها بعد معرفة الشكل الصريح للجهد (V(r ويمكن وضعها بالشكل:
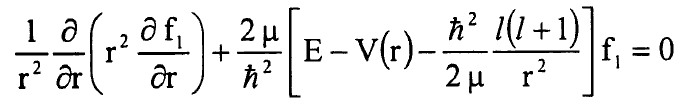....................(9)
الاكثر قراءة في الفيزياء الجزيئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
