Riemann defined the function 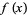 by

			(1)
			(2)
			(3)

(Hardy 1999, p. 30; Borwein et al. 2000; Havil 2003, pp. 189-191 and 196-197; Derbyshire 2004, p. 299), sometimes denoted 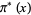,  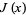(Edwards 2001, pp. 22 and 33; Derbyshire 2004, p. 298), or  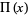(Havil 2003, p. 189). Note that this is not an infinite series since the terms become zero starting at 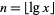, and where  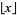is the floor function and  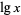is the base-2 logarithm. For 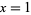, 2, ..., the first few values are 0, 1, 2, 5/2, 7/2, 7/2, 9/2, 29/6, 16/3, 16/3, ... (OEIS A096624 and A096625). As can be seen, when  is a prime, 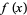 jumps by 1; when it is the square of a prime, it jumps by 1/2; when it is a cube of a prime, it jumps by 1/3; and so on (Derbyshire 2004, pp. 300-301), as illustrated above.

Amazingly, the prime counting function 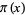 is related to  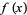by the Möbius transform

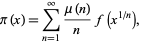(4)

where 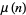 is the Möbius function (Riesel 1994, p. 49; Havil 2003, p. 196; Derbyshire 2004, p. 302). More amazingly still,  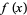is connected with the Riemann zeta function  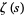by

(5)

(Riesel 1994, p. 47; Edwards 2001, p. 23; Derbyshire 2004, p. 309). 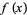 is also given by

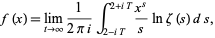(6)

where 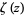 is the Riemann zeta function, and (5) and (6) form a Mellin transform pair.

Riemann (1859) proposed that

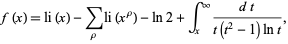(7)

where 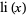 is the logarithmic integral and the sum is over all nontrivial zeros  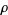of the Riemann zeta function  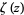(Mathews 1961, Ch. 10; Landau 1974, Ch. 19; Ingham 1990, Ch. 4; Hardy 1999, p. 40; Borwein et al. 2000; Edwards 2001, pp. 33-34; Havil 2003, p. 196; Derbyshire 2004, p. 328). Actually, since the sum of roots is only conditionally convergent, it must be summed in order of increasing  even when pairing terms 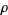 with their "twins" 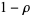, so

(8)

(Edwards 2001, pp. 30 and 33).

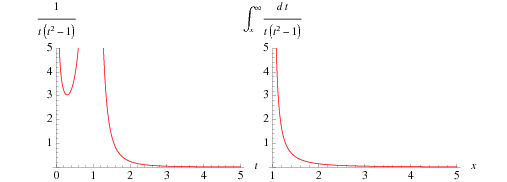
This formula was subsequently proved by Mangoldt (1895; Riesel 1994, p. 47; Edwards 2001, pp. 48 and 62-65). The integral on the right-hand side converges only for 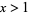, but since there are no primes less than 2, the only values of interest are for 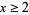. Since it is monotonic decreasing, the maximum therefore occurs at 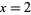, which has value

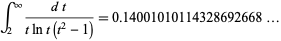(9)

(OEIS A096623; Derbyshire 2004, p. 329).

Riemann also considered the function

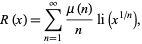(10)

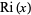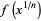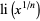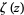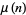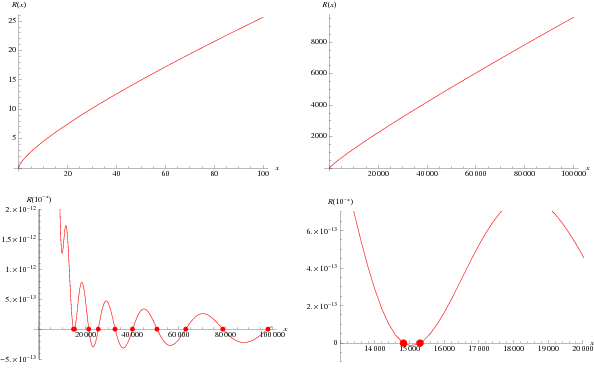
sometimes also denoted  (Borwein et al. 2000), obtained by replacing  in the Riemann function with the logarithmic integral , where  is the Riemann zeta function and  is the Möbius function (Hardy 1999, pp. 16 and 23; Borwein et al. 2000; Havil 2003, p. 198). 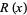 is plotted above, including on a semilogarithmic scale (bottom two plots), which illustrate the fact that  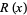has a series of zeros near the origin. These occur at  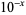for 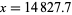 (OEIS A143530), 15300.7, 21381.5, 25461.7, 32711.9, 40219.6, 50689.8, 62979.8, 78890.2, 98357.8, ..., corresponding to  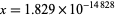(OEIS A143531), , , , , , , , , , ....

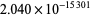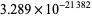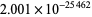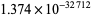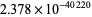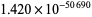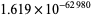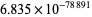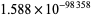The quantity 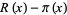 is plotted above.

This function is implemented in the Wolfram Language as RiemannR[x].

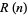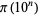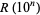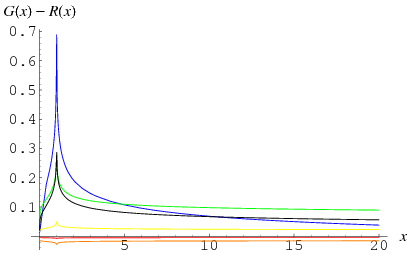
Ramanujan independently derived the formula for , but nonrigorously (Berndt 1994, p. 123; Hardy 1999, p. 23). The following table compares  and  for small 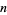. Riemann conjectured that  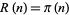(Knuth 1998, p. 382), but this was disproved by Littlewood in 1914 (Hardy and Littlewood 1918).

The Riemann prime counting function is identical to the Gram series

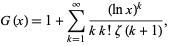(11)

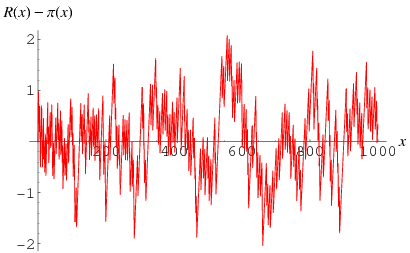
where 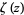 is the Riemann zeta function (Hardy 1999, pp. 24-25), but the Gram series is much more tractable for numeric computations. For example, the plots above show the differenc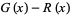e  where 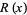 is computed using the Wolfram Language's built-in NSum command (black) and approximated using the first  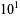(blue),  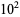(green),  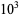(yellow),  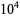(orange), and  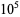(red) points.

In the table,  denotes the nearest integer function. Note that the values given by Hardy (1999, p. 26) for 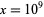 are incorrect.

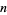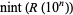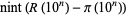Sloane	A057793	A057794
1	5	1
2	26	1
3	168	0
4	1227
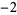5	9587
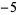6	78527	29
7	664667	88
8	5761552	97
9	50847455
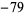10	455050683
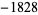11	4118052495
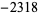12	37607910542

Riemann's function is related to the prime counting function by

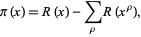(12)

where the sum is over all complex (nontrivial) zeros 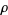 of 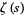 (Ribenboim 1996), i.e., those in the critical strip so , interpreted to mean

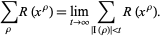(13)

However, no proof of the equality of (12) appears to exist in the literature (Borwein et al. 2000).

REFERENCES:

Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.

Hardy, G. H. and Littlewood, J. E. Acta Math. 41, 119-196, 1918.

Hardy, G. H. "The Series 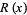." §2.3 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 42, 2003.

Ingham, A. E. The Distribution of Prime Numbers. London: Cambridge University Press, p. 83, 1990.

Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.

Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, 1974.

Mangoldt, H. von. "Zu Riemann's Abhandlung 'Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse.' " J. reine angew. Math. 114, 255-305, 1895.

Mathews, G. B. Ch. 10 in Theory of Numbers. New York: Chelsea, 1961.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 224-225, 1996.

Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859. Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972. Also reprinted in English translation in Edwards, H. M. Appendix. Riemann's Zeta Function. New York: Dover, pp. 299-305, 2001.

Riemann, B. "Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe." Reprinted in Gesammelte math. Abhandlungen. New York: Dover, pp. 227-264, 1957.

Riesel, H. and Göhl, G. "Some Calculations Related to Riemann's Prime Number Formula." Math. Comput. 24, 969-983, 1970.

Riesel, H. "The Riemann Prime Number Formula." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 50-52, 1994.

Sloane, N. J. A. Sequences A057793, A057794, A096623, A096624, A096625, A143530, A143531 in "The On-Line Encyclopedia of Integer Sequences."

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 28-29 and 362-372, 1991.