Noble Number
المؤلف:
Hardy, G. H. and Wright, E. M.
المصدر:
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press
الجزء والصفحة:
...
10-5-2020
1302
Noble Number
A noble number 
is defined as an irrational number having a continued fraction that becomes an infinite sequence of 1s at some point,
The prototype is the inverse of the golden ratio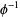 
, whose continued fraction is composed entirely of 1s (except for the 
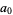term), ![[0,1^_]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline4.gif)
.
Any noble number can be written as
where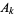 
and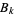 
are the numerator and denominator of the 
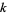th convergent of ![[0,a_1,a_2,...,a_n]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline8.gif)
.
The noble numbers are a subset of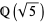 
but not a subfield, since there is no subfield lying properly between 
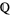and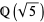 
. To see this, consider 
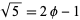, which must be contained in the same field as 
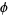but is not a noble number since its continued fraction is ![[2,4^_]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline14.gif)
.
REFERENCES:
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 236, 1979.
Schroeder, M. "Noble and Near Noble Numbers." In Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, pp. 392-394, 1991.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
