Apéry's constant is defined by

(OEIS A002117) where 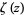 is the Riemann zeta function.  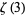was computed to  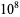decimal digits by E. Weisstein on Sep. 16, 2013.

The Earls sequence (starting position of 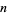 copies of the digit 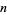) for 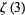 is given for 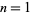, 2, ... by 10, 57, 3938, 421, 41813, 1625571, 4903435, 99713909, ... (OEIS A229074).

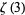-constant prime occur for 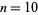, 55, 109, 141, ... (OEIS A119334), corresponding to the primes 1202056903, 1202056903159594285399738161511449990764986292340498881, ... (OEIS A119333).

The starting positions of the first occurrence of 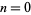, 1, 2, ... in the decimal expansion of  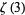(not including the initial 0 to the left of the decimal point) are 3, 1, 2, 10, 16, 6, 7, 23, 18, 8, ... (OEIS A229187).

Scanning the decimal expansion of 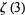 until all 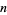-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 7, 89, 211, 2861, 43983, 292702, 8261623, ... (OEIS A036902), which end at digits 23, 457, 7839, 83054, 1256587, 13881136, 166670757, ... (OEIS A036906).

The digit sequences 0123456789 and 9876543210 do not occur in the first 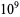 digits (E. Weisstein, Sep. 17, 2013).

It is not known if 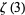 is normal (Bailey and Crandall 2003). but the following table giving the counts of digits in the first  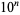terms shows that the decimal digits are very uniformly distributed up to at least .

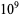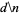	OEIS	10	100
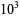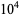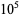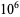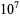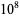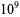0	A000000	3	9	108	990	9910	99761	1000416	9999248	100001073
1	A000000	1	11	104	1024	10037	100273	1000484	10000163	99996430
2	A000000	2	9	109	1007	10061	100012	1001036	10005579	99985752
3	A000000	1	11	106	1010	9961	99894	998032	10000695	100007728
4	A000000	0	8	76	953	9957	99904	998174	9991603	99994148
5	A000000	1	13	108	1006	9933	100399	1002043	10003610	99999279
6	A000000	1	7	90	1001	9967	99525	999818	10003630	100014221
7	A000000	0	6	113	1064	10253	100616	1000198	9995077	99993290
8	A000000	0	12	90	981	9931	99675	999969	10001192	100009336
9	A000000	1	14	96	964	9990	99941	999830	9999203	99998743

REFERENCES:

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Preprint dated Feb. 22, 2003 available at http://www.nersc.gov/~dhbailey/dhbpapers/bcnormal.pdf.

Sloane, N. J. A. Sequences A002117, A036902, A036906, A119333, A119334, A229074, and A229187 in "The On-Line Encyclopedia of Integer Sequences."