
Modular Equation
 المؤلف:
Borwein, J. M. and Borwein, P. B
المؤلف:
Borwein, J. M. and Borwein, P. B
 المصدر:
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley
المصدر:
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley
 الجزء والصفحة:
...
الجزء والصفحة:
...
 24-12-2019
24-12-2019
 1048
1048
Modular Equation
The modular equation of degree 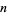 gives an algebraic connection of the form
gives an algebraic connection of the form
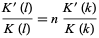 |
(1)
|
between the transcendental complete elliptic integrals of the first kind with moduli 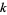 and
and 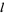 . When
. When 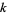 and
and 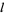 satisfy a modular equation, a relationship of the form
satisfy a modular equation, a relationship of the form
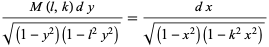 |
(2)
|
exists, and 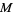 is called the multiplier. In general, if
is called the multiplier. In general, if 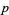 is an odd prime, then the modular equation is given by
is an odd prime, then the modular equation is given by
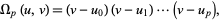 |
(3)
|
where
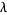 is a elliptic lambda function, and
is a elliptic lambda function, and
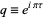 |
(6)
|
(Borwein and Borwein 1987, p. 126), where  is the half-period ratio. An elliptic integral identity gives
is the half-period ratio. An elliptic integral identity gives
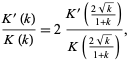 |
(7)
|
so the modular equation of degree 2 is
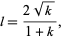 |
(8)
|
which can be written as
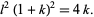 |
(9)
|
A few low order modular equations written in terms of 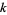 and
and 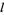 are
are
In terms of 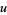 and
and 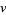 ,
,
where
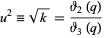 |
(17)
|
and
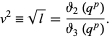 |
(18)
|
Here, 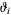 are Jacobi theta functions.
are Jacobi theta functions.
A modular equation of degree 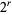 for
for 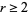 can be obtained by iterating the equation for
can be obtained by iterating the equation for 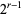 . Modular equations for prime
. Modular equations for prime 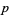 from 3 to 23 are given in Borwein and Borwein (1987).
from 3 to 23 are given in Borwein and Borwein (1987).
Quadratic modular identities include
![(theta_3(q))/(theta_3(q^4))-1=[(theta_3^2(q^2))/(theta_3^2(q^4))-1]^(1/2).](http://mathworld.wolfram.com/images/equations/ModularEquation/NumberedEquation10.gif) |
(19)
|
Cubic identities include
![[3(theta_2(q^9))/(theta_2(q))-1]^3=9(theta_2^4(q^3))/(theta_2^4(q))-1](http://mathworld.wolfram.com/images/equations/ModularEquation/NumberedEquation11.gif) |
(20)
|
![[3(theta_3(q^9))/(theta_3(q))-1]^3=9(theta_3^4(q^3))/(theta_3^4(q))-1](http://mathworld.wolfram.com/images/equations/ModularEquation/NumberedEquation12.gif) |
(21)
|
![[3(theta_4(q^9))/(theta_4(q))-1]^3=9(theta_4^4(q^3))/(theta_4^4(q))-1.](http://mathworld.wolfram.com/images/equations/ModularEquation/NumberedEquation13.gif) |
(22)
|
A seventh-order identity is
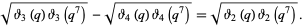 |
(23)
|
From Ramanujan (1913-1914),
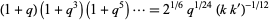 |
(24)
|
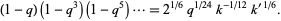 |
(25)
|
When 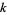 and
and 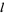 satisfy a modular equation, a relationship of the form
satisfy a modular equation, a relationship of the form
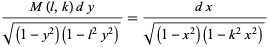 |
(26)
|
exists, and 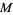 is called the multiplier. The multiplier of degree
is called the multiplier. The multiplier of degree 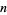 can be given by
can be given by
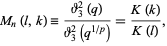 |
(27)
|
where 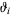 is a Jacobi theta function and
is a Jacobi theta function and 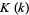 is a complete elliptic integral of the first kind.
is a complete elliptic integral of the first kind.
The first few multipliers in terms of 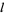 and
and 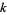 are
are
In terms of the 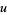 and
and 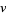 defined for modular equations,
defined for modular equations,
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 127-132, 1987.
Hanna, M. "The Modular Equations." Proc. London Math. Soc. 28, 46-52, 1928.
Ramanujan, S. "Modular Equations and Approximations to 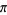 ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


